题目内容
已知直线l1：3x-
y+1=0与直线l2：
x-3y+2=0，则l1与l2的夹角为（ ）
| 3 |
| 3 |
| A、150° | B、120° |
| C、60° | D、30° |
考点：两直线的夹角与到角问题
专题：直线与圆
分析：先根据直线的斜率求出直线的倾斜角，再利用两条直线的倾斜角的大小求出这两条直线的夹角．
解答：
解：因为直线l1的斜率为
，故倾斜角为60°，直线l2的斜率为
，倾斜角为30°，故两直线的夹角为30°，
故选：D．
| 3 |
| ||
| 3 |
故选：D．
点评：本题考查直线的斜率和倾斜角的关系，由两条直线的倾斜角求出两条直线的夹角．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
函数f（x）=
的图象大致为（ ）
| 2xcos2x |
| 22x-1 |
A、 |
B、 |
C、 |
D、 |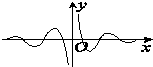
甲、乙两人轮流投一枚均匀硬币，甲先投，谁先得到正面谁获胜，求投币不超过四次即决定胜负的概率（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中错误的是（ ）
| A、命题“若p则q”与命题“若￢q则￢p”互为逆否命题 | ||
| B、y=f（x），x∈R，满足f（x+2）=-f（x），则该函数是周期为4的函数 | ||
| C、命题p：?x∈[0，1]，ex≥1，命题q：?x∈R，x2+x+1＜0，则p∨q为真 | ||
D、若实数x，y∈[0，1]，则满足x2+y2＞1的概率为
|
设i为虚数单位，若z=（
）2012+（
）2013，则它的共轭复数
为（ ）
| 1+i |
| 1-i |
| 1-i |
| 1+i |
. |
| z |
| A、1-i | B、-1+i |
| C、1+i | D、-1-i |
在（
-
）n的二项展开式中，只有第四项的二项式系数最大，则展开式中常数项是（ ）
| x |
| 2 |
| 1 |
| x2 |
| A、-15 | ||
| B、15 | ||
C、-
| ||
D、
|
已知集合A={1，2，3，4，5}，B={y|y=2x-1，x∈A}，则A∩B=（ ）
| A、{2，4} |
| B、{1，3，5} |
| C、{1，2，3，5} |
| D、{1，2，3，4，5} |
已知tanθ+
=2，则sinθ+cosθ等于（ ）
| 1 |
| tanθ |
| A、2 | ||
B、
| ||
C、-
| ||
D、±
|