题目内容

已知函数f（x）是二次函数且满足f（x+1）+f（x-1）=x2-2x-1，求函数f（x）解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由题意设f（x）=ax2+bx+c，a≠0，代入已知式子比较系数可得a、b、c的方程组，解方程组可得函数解析式．
解答： 解：由题意设f（x）=ax2+bx+c，a≠0，
则f（x+1）+f（x-1）=a（x+1）2+b（x+1）+c+a（x-1）2+b（x-1）+c
=2ax2+2bx+2a+2c=x2-2x-1，
∴2a=1，2b=-2，2a+2c=-1，
解得a=
1
2
，b=-1，c=-1，
∴f（x）解析式为：f（x）=
1
2
x2-x-1
点评：本题考查函数解析式的求解，涉及待定系数法，属基础题．
练习册系列答案
相关题目
设数列{3n-1an}的前n项和为Sn，且Sn=
n
3
，a∈N*．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=
n
an
，求数列{bn}的前n项和Tn．
i是虚数单位，i（-1+2i）=（　　）
A、i+2B、i-2
C、-2-iD、2-i
已知椭圆E：
x2
100
+
y2
25
=1的上顶点为A，直线y=-4交椭圆E于点B，C（点B在点C的左侧），点P在椭圆E上．
（Ⅰ）求以原点为顶点，椭圆的右焦点为焦点的抛物线的方程；
（Ⅱ）若四边形ABCD为梯形，求点P的坐标；
（Ⅲ）若
BP
=m•
BA
+n•
BC
（m，n为实数），求m+n的最大值及对应的P的坐标．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
1
2
，以原点O为圆心，椭圆的短半轴长为半径的圆与直线x-y+
6
=0相切．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线L：y=kx+m与椭圆C相交于A、B两点，且kOA•kOB=-
b2
a2
，求证：△AOB的面积为定值．
已知定义在R上的函数f（x）=2x+
1
2x

（1）判断f（x）为奇偶性；
（2）证明f（x）函数在[0，+∞）上单调递增．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦距为2，且过点（1，
2
2
），右焦点为F2．设A，B是C上的两个动点，线段AB的中点M的横坐标为-
1
2
，线段AB的中垂线交椭圆C于P，Q两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求
F2P
•
F2Q
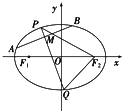的取值范围．
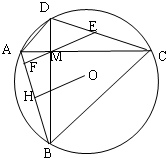如图，四边形ACBD内接于圆O，对角线AC与BD相交于M，AC⊥BD，E是DC中点连结EM交AB于F，作OH⊥AB于H，求证：
（1）EF⊥AB          
（2）OH=ME．
在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b≥1)过点P（2，1），且离心率e=
3
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线的l的斜率为
1
2
，直线l与椭圆C交于A、B两点．求△PAB面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网