题目内容
已知函数f（x）=
+2sinx．
（1）求函数f（x）的定义域和最小正周期；
（2）若f（α）=2，α∈[0，π]，求f（α+
）的值．
| sin2x |
| sinx |
（1）求函数f（x）的定义域和最小正周期；
（2）若f（α）=2，α∈[0，π]，求f（α+
| π |
| 12 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：计算题,三角函数的图像与性质
分析：（1）由sinx≠0，即可求得f（x）的定义域，利用三角恒等变换可求得f（x）=2
sin（
+x），从而可求其最小正周期；
（2）由f（α）=2，α∈[0，π]，可求得α=
，于是可求得f（α+
）的值．
| 2 |
| π |
| 4 |
（2）由f（α）=2，α∈[0，π]，可求得α=
| π |
| 2 |
| π |
| 12 |
解答：
解：（1）∵sinx≠0解得x≠kπ（k∈Z），
∴函数f（x）的定义域为{x|x≠kπ（k∈Z）}------------------------（2分）
∵f（x）=
+2sinx=2cosx+2sinx=2
sin（
+x）---（4分）
∴f（x）的最小正周期T=
=2π-----------------------------------（6分）
（2）∵f（α）=2，
∴cosα+sinα=1，
∴（cosα+sinα）2=1，即2sinαcosα=0，---------------------（8分）
∵α∈[0，π]，且sinα≠0，
∴α=
------------------------------------（10分）
∴f（α+
）=2
sin（
+α+
）=2
sin
=
------------------------------------（12分）
∴函数f（x）的定义域为{x|x≠kπ（k∈Z）}------------------------（2分）
∵f（x）=
| sin2x |
| sinx |
| 2 |
| π |
| 4 |
∴f（x）的最小正周期T=
| 2π |
| 1 |
（2）∵f（α）=2，
∴cosα+sinα=1，
∴（cosα+sinα）2=1，即2sinαcosα=0，---------------------（8分）
∵α∈[0，π]，且sinα≠0，
∴α=
| π |
| 2 |
∴f（α+
| π |
| 12 |
| 2 |
| π |
| 4 |
| π |
| 12 |
| 2 |
| 5π |
| 6 |
| 2 |
点评：本题考查三角函数中的恒等变换应用，考查正弦函数的定义域与周期，考查运算求解能力，属于中档题．
练习册系列答案
特高级教师点拨系列答案
相关题目
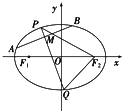已知椭圆C：
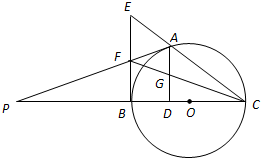如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．
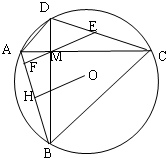如图，四边形ACBD内接于圆O，对角线AC与BD相交于M，AC⊥BD，E是DC中点连结EM交AB于F，作OH⊥AB于H，求证：