题目内容
甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏,已知甲每次投中的概率为
,乙每次投中的概率为
,求游戏结束时.
(Ⅰ)甲、己投篮次数之和为3的概率;
(Ⅱ)乙投篮次数不超过1次的概率.
| 1 |
| 4 |
| 1 |
| 3 |
(Ⅰ)甲、己投篮次数之和为3的概率;
(Ⅱ)乙投篮次数不超过1次的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题:概率与统计
分析:(Ⅰ)由题意可得,第一次甲投,没有投中,概率为
,第二次乙投,也没有投中,概率为
,第三次甲投,投中了,概率为
,再根据相互独立事件的概率乘法公式求得结果.
(Ⅱ)先求出第一次甲投中的概率;甲第一次投有投中、第二次乙没有投中,第三次甲投中了的概率;甲第一次没有投中,第二次乙投中的概率,相加,即得所求.
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
(Ⅱ)先求出第一次甲投中的概率;甲第一次投有投中、第二次乙没有投中,第三次甲投中了的概率;甲第一次没有投中,第二次乙投中的概率,相加,即得所求.
解答:
解:(Ⅰ)由题意可得,甲、己投篮次数之和为3,说明第一次甲投,没有投中,概率为 1-
=
,
第二次乙投,也没有投中,概率为1-
=
,第三次甲投,投中了,概率为
,
再根据相互独立事件的概率乘法公式可得甲、己投篮次数之和为3的概率为
×
×
=
.
(Ⅱ)若甲第一次投中了,则乙投球次数为零,概率为
.
若甲第一次投有投中,第二次乙投没有投中,第三次甲投中了,由(Ⅰ)知概率为
.
若甲第一次没有投中,第二次乙投中了,概率为(1-
)
=
.
故乙投篮次数不超过1次的概率为
+
+
=
.
| 1 |
| 4 |
| 3 |
| 4 |
第二次乙投,也没有投中,概率为1-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
再根据相互独立事件的概率乘法公式可得甲、己投篮次数之和为3的概率为
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 8 |
(Ⅱ)若甲第一次投中了,则乙投球次数为零,概率为
| 1 |
| 4 |
若甲第一次投有投中,第二次乙投没有投中,第三次甲投中了,由(Ⅰ)知概率为
| 1 |
| 8 |
若甲第一次没有投中,第二次乙投中了,概率为(1-
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
故乙投篮次数不超过1次的概率为
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 8 |
点评:本题主要考查相互独立事件的概率乘法公式的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
i是虚数单位,i(-1+2i)=( )
| A、i+2 | B、i-2 |
| C、-2-i | D、2-i |
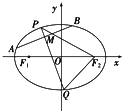 已知椭圆C:
已知椭圆C: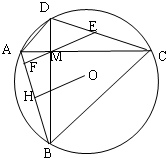 如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证:
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证: