题目内容
9．已知向量$\overrightarrow a=（1，1），\overrightarrow b=（2，-3）$若$λ\overrightarrow a-2\overrightarrow b$与$\overrightarrow a$垂直，求λ的值；若$\overrightarrow a-2k\overrightarrow b$与$\overrightarrow a+\overrightarrow b$平行，求k的值．分析 （1）利用向量垂直与数量积的关系即可得出．
（2）利用向量共线定理即可得出．
解答 解：（1）$λ\overrightarrow a-2\overrightarrow b$=（λ-4，λ+6），
∵$λ\overrightarrow a-2\overrightarrow b$与$\overrightarrow a$垂直，∴（$λ\overrightarrow a-2\overrightarrow b$）•$\overrightarrow a$=λ-4+λ+6=，
解得λ=-1．
（2）$\overrightarrow a-2k\overrightarrow b$=（1-4k，1+6k），
$\overrightarrow a+\overrightarrow b$=（3，-1）．
∵$\overrightarrow a-2k\overrightarrow b$与$\overrightarrow a+\overrightarrow b$平行，∴3（1+6k）+（1-4k）=0，
解得k=-$\frac{2}{7}$．
点评 本题考查了向量垂直与数量积的关系、向量共线定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
19．
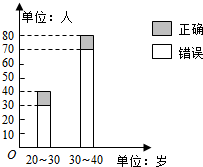“开门大吉”是某电视台推出的游戏节目，选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金，在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（Ⅰ）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关；说明你的理由：（下面的临界值表供参考）
（Ⅱ）现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
“开门大吉”是某电视台推出的游戏节目，选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金，在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．（Ⅰ）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关；说明你的理由：（下面的临界值表供参考）
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
20．将一枚质地均匀的骰子抛掷两次，落地时朝上的点数之和为6的概率为（ ）
| A． | $\frac{5}{36}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{9}$ |
4．$f（x）={e^{-{x^2}+3x+1}}$，求f′（x）（ ）
| A． | f（x）=（-2x+3）ex | B． | f（x）=e-2x+3 | ||
| C． | $f（x）={e^{-{x^2}+3x+1}}$ | D． | $f（x）=（-2x+3）{e^{-{x^2}+3x+1}}$ |