题目内容
14.已知椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$,直线l:4x-5y+40=0.椭圆上是否存在一点,它到直线l的距离最小?最小距离是多少?分析 设出平行线方程,利用直线与椭圆相切,求出切线方程,然后求解平行线距离即可.
解答 解:设直线m:4x-5y+λ=0平行于直线l
由方程组:$\left\{\begin{array}{l}\frac{x^2}{25}+\frac{y^2}{9}=1\\ 4x-5y+λ=0\end{array}\right.$
消去y得:25x2+8kx+k2-225=0
由△=0可得:64k2-4×25(k2-225)=0
解得:k1=25或k2=-25
取k=25时距离最近,$d=\frac{|40-25|}{{\sqrt{{4^2}+{5^2}}}}=\frac{15}{41}\sqrt{41}$.
点评 本题考查椭圆与直线的位置关系的应用,考查椭圆与直线相切,函数与方程的思想的应用,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.执行如图所示的程序框图,如果输入的a,b分别为56,140,则输出的a=( )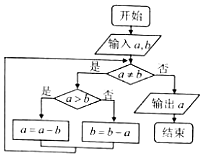

| A. | 0 | B. | 7 | C. | 14 | D. | 28 |
5.如图是求12+22+32+…+1002的程序框图,则图中的①②分别是( )
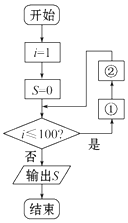

| A. | ①S=S+i ②i=i+1 | B. | ①S=S+i2 ②i=i+1 | C. | ①i=i+1 ②S=S+i | D. | ①i=i+1 ②S=S+i2 |

 一个几何体的三视图如图所示(单位:m),则该几何体的体积为15m3.
一个几何体的三视图如图所示(单位:m),则该几何体的体积为15m3.