题目内容
20．将一枚质地均匀的骰子抛掷两次，落地时朝上的点数之和为6的概率为（ ）| A． | $\frac{5}{36}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{9}$ |
分析 先求出基本事件总数n=6×6=36，再利用列举法求出落地时朝上的点数之和为6包含的基本事件的个数，由此能求出落地时朝上的点数之和为6的概率．
解答 解：将一枚质地均匀的骰子抛掷两次，
基本事件总数n=6×6=36，
落地时朝上的点数之和为6包含的基本事件有：
（1，5），（5，1），（2，4），（4，2），（3，3），共5个，
∴落地时朝上的点数之和为6的概率为p=$\frac{5}{36}$．
故选：A．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．已知复数z满足1+i=（1-i）2z，则z的共轭复数在复平面内所对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
15．若复数z=2-i+i2，则z2=（ ）
| A． | 2 | B． | 2i | C． | -2i | D． | $\sqrt{2}$ |
5．如图是求12+22+32+…+1002的程序框图，则图中的①②分别是（ ）
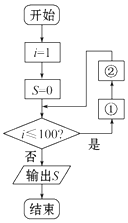
| A． | ①S=S+i ②i=i+1 | B． | ①S=S+i2 ②i=i+1 | C． | ①i=i+1 ②S=S+i | D． | ①i=i+1 ②S=S+i2 |
12．圆ρ=r与圆ρ=-2rsin（θ+$\frac{π}{4}$）（r＞0）的公共弦所在直线的方程为（ ）
| A． | 2ρ（sin θ+cos θ）=r | B． | 2ρ（sin θ+cos θ）=-r | ||
| C． | $\sqrt{2}$ρ（sin θ+cos θ）=r | D． | $\sqrt{2}$ρ（sin θ+cos θ）=-r |