题目内容
设两个独立事件A，B都不发生的概率为
．则A与B都发生的概率值可能为（ ）
| 1 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相互独立事件的概率乘法公式
专题：计算题,概率与统计
分析：不妨设A不发生的概率为x，B不发生的概率为y，则xy=
，A与B都发生的概率=（1-x）（1-y）=
-（x+y）≤
，即可得出结论．
| 1 |
| 9 |
| 10 |
| 9 |
| 4 |
| 9 |
解答：
解：因为AB是独立事件，不妨设A不发生的概率为x，B不发生的概率为y，则xy=
．
因为x，y的范围是0＜x，y≤1，x+y=x+
≥
，
所以A与B都发生的概率=（1-x）（1-y）=
-（x+y）≤
故选：D．
| 1 |
| 9 |
因为x，y的范围是0＜x，y≤1，x+y=x+
| 1 |
| 9x |
| 2 |
| 3 |
所以A与B都发生的概率=（1-x）（1-y）=
| 10 |
| 9 |
| 4 |
| 9 |
故选：D．
点评：本题考查相互独立事件的概率乘法公式，开车基本不等式的运用，属于基础题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图，△OAB是等腰三角形，P是底边AB延长线上一点，且PO=3，PA•PB=4，则腰长OA=已知数列{an}满足a1=2，an+1=
，则a2014等于（ ）
| 1+an |
| 1-an |
| A、2 | ||
B、-
| ||
| C、-3 | ||
D、
|
“函数y=ax单调递减”是“lna＜1”的什么条件．（ ）
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
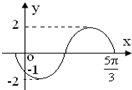已知函数f（x）=2sin（ωx+φ）（ω＞0，-π＜φ＜π）图象的一部分（如图所示），则ω与φ的值分别为（ ）A、
| ||||
B、1，-
| ||||
C、
| ||||
D、
|
等比数列{an}中，a1=2，a8=4，函数f（x）=x（x-a4）（x-a5），则[f′（0）]4=（ ）
| A、216 |
| B、212 |
| C、28 |
| D、24 |
等差数列的相邻4项分别是a+1，a+3，b，a+b，那么a，b的值依次为（ ）
| A、2，7 | B、1，6 |
| C、0，5 | D、无法确定 |