题目内容
求定积分
f（x）dx，其中f（x）=
．
| ∫ | 1 -1 |
|
考点：定积分
专题：导数的概念及应用
分析：根据积分计算公式，求出被积函数的原函数，再根据微积分基本定理加以计算，即可得到本题答案．
解答：
解：
f（x）dx=
（sinx-1）dx+
x2dx
=（-cosx-x）
+
x3
=cos1-2+
=cos1-
| ∫ | 1 -1 |
| ∫ | 0 -1 |
| ∫ | 1 0 |
=（-cosx-x）
| | | 0 -1 |
| 1 |
| 3 |
| | | 1 0 |
=cos1-2+
| 1 |
| 3 |
=cos1-
| 5 |
| 3 |
点评：本题求一个函数的原函数并求定积分值，考查定积分的运算和微积分基本定理等知识，属于基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
方程1-z4=0在复数范围内的根共有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
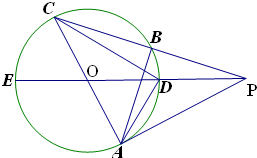如图，PA是⊙O的切线，PE过圆心0，AC为⊙O的直径，PC与⊙O相交于B、C两点，连接AB、CD．
在线路中，各原件能否正常工作是相互独立的，已知原件a，b，c，d，e能正常工作的概率是0.9，0.95，0.7，0.8，0.85，求线路畅通的概率．