题目内容
设a1=1,an+1=
+b(n∈N*)
(Ⅰ)若b=1,求a2,a3及数列{an}的通项公式;
(Ⅱ)若b=-1,问:是否存在实数c使得a2n<c<a2n+1对所有的n∈N*成立,证明你的结论.
|
(Ⅰ)若b=1,求a2,a3及数列{an}的通项公式;
(Ⅱ)若b=-1,问:是否存在实数c使得a2n<c<a2n+1对所有的n∈N*成立,证明你的结论.
考点:数学归纳法,数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(Ⅰ)若b=1,利用an+1=
+b,可求a2,a3;证明{(an-1)2}是首项为0,公差为1的等差数列,即可求数列{an}的通项公式;
(Ⅱ)设f(x)=
-1,则an+1=f(an),令c=f(c),即c=
-1,解得c=
.用数学归纳法证明加强命题a2n<c<a2n+1<1即可.
|
(Ⅱ)设f(x)=
| (x-1)2+1 |
| (c-1)2+1 |
| 1 |
| 4 |
解答:
解:(Ⅰ)∵a1=1,an+1=
+b,b=1,
∴a2=2,a3=
+1;
又(an+1-1)2=(an-1)2+1,
∴{(an-1)2}是首项为0,公差为1的等差数列;
∴(an-1)2=n-1,
∴an=
+1(n∈N*);
(Ⅱ)设f(x)=
-1,则an+1=f(an),
令c=f(c),即c=
-1,解得c=
.
下面用数学归纳法证明加强命题a2n<c<a2n+1<1.
n=1时,a2=f(1)=0,a3=f(0)=
-1,∴a2<c<a3<1,成立;
设n=k时结论成立,即a2k<c<a2k+1<1
∵f(x)在(-∞,1]上为减函数,
∴c=f(c)>f(a2k+1)>f(1)=a2,
∴1>c>a2k+2>a2,
∴c=f(c)<f(a2k+2)<f(a2)=a3<1,
∴c<a2k+3<1,
∴a2(k+1)<c<a2(k+1)+1<1,即n=k+1时结论成立,
综上,c=
使得a2n<c<a2n+1对所有的n∈N*成立.
|
∴a2=2,a3=
| 2 |
又(an+1-1)2=(an-1)2+1,
∴{(an-1)2}是首项为0,公差为1的等差数列;
∴(an-1)2=n-1,
∴an=
| n-1 |
(Ⅱ)设f(x)=
| (x-1)2+1 |
令c=f(c),即c=
| (c-1)2+1 |
| 1 |
| 4 |
下面用数学归纳法证明加强命题a2n<c<a2n+1<1.
n=1时,a2=f(1)=0,a3=f(0)=
| 2 |
设n=k时结论成立,即a2k<c<a2k+1<1
∵f(x)在(-∞,1]上为减函数,
∴c=f(c)>f(a2k+1)>f(1)=a2,
∴1>c>a2k+2>a2,
∴c=f(c)<f(a2k+2)<f(a2)=a3<1,
∴c<a2k+3<1,
∴a2(k+1)<c<a2(k+1)+1<1,即n=k+1时结论成立,
综上,c=
| 1 |
| 4 |
点评:本题考查数列递推式,考查数列的通项,考查数学归纳法,考查学生分析解决问题的能力,难度大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线C的离心率为2,焦点为F1、F2,点A在C上,若|F1A|=2|F2A|,则cos∠AF2F1=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设x,y满足约束条件
,则z=x+2y的最大值为( )
|
| A、8 | B、7 | C、2 | D、1 |
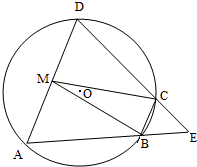 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE. 如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β.
如图,某公司要在A、B两地连线上的定点C处建造广告牌CD,其中D为顶端,AC长35米,CB长80米,设点A、B在同一水平面上,从A和B看D的仰角分别为α和β.