题目内容
某实验室一天的温度（单位：℃）随时间t（单位：h）的变化近似满足函数关系：f（t）=10-
cos
t-sin
t，t∈[0，24）．
（Ⅰ）求实验室这一天上午8时的温度；
（Ⅱ）求实验室这一天的最大温差．
| 3 |
| π |
| 12 |
| π |
| 12 |
（Ⅰ）求实验室这一天上午8时的温度；
（Ⅱ）求实验室这一天的最大温差．
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（Ⅰ）直接根据f（t）的解析式求得f（8）的值．
（Ⅱ）根据f（t）=10-2sin（
+
t），t∈[0，24），求得函数f（t）取得最大值和最小值，从而得到这一天的最大温差．
（Ⅱ）根据f（t）=10-2sin（
| π |
| 3 |
| π |
| 12 |
解答：
解：（Ⅰ）∵f（t）=10-
cos
t-sin
t，t∈[0，24）．
∴f（8）=10-
cos
-sin
=10-
×（-
）-
=10，
故实验室这一天上午8时的温度为10℃．
（Ⅱ）∵f（t）=10-
cos
t-sin
t=10-2sin（
+
t），t∈[0，24）．
∴
＜
+
t＜
，故当
+
t=
，即t=14时，函数f（t）取得最大值为10+2=12，
当
+
t=
，即t=2时，函数f（t）取得最小值为10-2=8，
故实验室这一天的最大温差为12-8=4℃．
| 3 |
| π |
| 12 |
| π |
| 12 |
∴f（8）=10-
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
故实验室这一天上午8时的温度为10℃．
（Ⅱ）∵f（t）=10-
| 3 |
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
∴
| π |
| 3 |
| π |
| 3 |
| π |
| 12 |
| 7π |
| 3 |
| π |
| 3 |
| π |
| 12 |
| 3π |
| 2 |
当
| π |
| 3 |
| π |
| 12 |
| π |
| 2 |
故实验室这一天的最大温差为12-8=4℃．
点评：本题主要考查函数y=Asin（ωx+φ）的图象特征，正弦函数的值域，属于中档题．
练习册系列答案
相关题目
定积分
（2x+ex）dx的值为（ ）
| ∫ | 1 0 |
| A、e+2 | B、e+1 |
| C、e | D、e-1 |
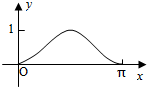
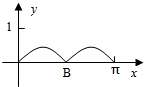
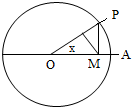如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P做直线OA的垂线，垂足为M，将点M到直线OP的距离表示为x的函数f（x），则y=f（x）在[0，π]的图象大致为（ ）
