题目内容
2.已知函数$f(x)=2sin(2x+\frac{π}{6})$.(Ⅰ)求函数f(x)在区间$[-\frac{π}{6},\frac{π}{6}]$上的最大值和最小值;
(Ⅱ)求函数f(x)的单调递增区间.
分析 (Ⅰ)由x的范围结合三角函数的值域可得;
(Ⅱ)解$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$可得函数f(x)单调递增区间.
解答 解:(Ⅰ)∵$-\frac{π}{6}≤x≤\frac{π}{6}$,∴$-\frac{π}{6}≤2x+\frac{π}{6}≤\frac{π}{2}$,
∴$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,∴$-1≤2sin(2x+\frac{π}{6})≤2$,
∴当$2x+\frac{π}{6}=\frac{π}{2}$即$x=\frac{π}{6}$时,函数f(x)的最大值为2;
当$2x+\frac{π}{6}=-\frac{π}{6}$即$x=-\frac{π}{6}$时,函数f(x)的最小值为-1;
(Ⅱ)由$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$可得$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}$,
∴函数f(x)单调递增区间为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
点评 本题考查正弦函数的图形化额单调性以及最值,属基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
10.设$a={(\frac{1}{2})^{2.5}},b={(2.5)^0},c={2^{2.5}}$,则( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
7.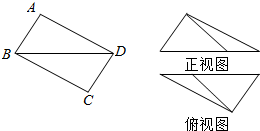 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{25}$ | D. | $\frac{36}{25}$ |
 如图,靠山有一个水库,某人先从水坝的底部A测得水坝对面的山顶P的仰角为40°,再沿坝面向上走80米到水坝的顶部B测得∠ABP=56°,若坝面与水平面所成的锐角为30°,则山高为176米;(结果四舍五入取整)
如图,靠山有一个水库,某人先从水坝的底部A测得水坝对面的山顶P的仰角为40°,再沿坝面向上走80米到水坝的顶部B测得∠ABP=56°,若坝面与水平面所成的锐角为30°,则山高为176米;(结果四舍五入取整)