题目内容
12.已知向量$\overrightarrow{m}$=($\sqrt{3}$cos$\frac{x}{2}$,cos$\frac{x}{2}$),$\overrightarrow{n}$=(sin$\frac{x}{2}$,cos$\frac{x}{2}$),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)在锐角△ABC中,已知A=$\frac{π}{3}$,求f(B)的取值范围.
分析 (1)利用数量积公式及三角函数公式化简f(x).
(2)求出B的范围,结合正弦函数性质得出f(B)的范围.
解答 解:(1)f(x)=$\sqrt{3}$cos$\frac{x}{2}$sin$\frac{x}{2}$+cos2$\frac{x}{2}$=$\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx+$\frac{1}{2}$=sin(x+$\frac{π}{6}$)+$\frac{1}{2}$,
∴f(x)的最小正周期T=2π.
(2)f(B)=sin(B+$\frac{π}{6}$)+$\frac{1}{2}$.
∵△ABC是锐角三角形,A=$\frac{π}{3}$,∴B∈($\frac{π}{6}$,$\frac{π}{2}$),∴$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,
∴当B+$\frac{π}{6}$=$\frac{π}{2}$时,f(B)取得最大值$\frac{3}{2}$,
B+$\frac{π}{6}$=$\frac{π}{3}$时,f(B)取得最小值$\frac{\sqrt{3}+1}{2}$.
∴f(B)的取值范围是($\frac{\sqrt{3}+1}{2}$,$\frac{3}{2}$].
点评 本题考查了三角函数的性质及化简求值,要记住常用公式及解题步骤,属于中档题.

练习册系列答案
相关题目
7.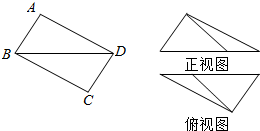 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{25}$ | D. | $\frac{36}{25}$ |
17.不等式组$\left\{\begin{array}{l}y≥0\\ x+3y≤4\\ 3x+y≥4\end{array}\right.$,所表示的平面区域的面积等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
2.下列条件使M与A,B,C一定共面的是( )
| A. | $\overrightarrow{OM}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OM}$+$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$ | ||
| C. | $\overrightarrow{OM}$=$\frac{1}{5}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | $\overrightarrow{MA}$+$\overrightarrow{MB}$+$\overrightarrow{MC}$=$\overrightarrow{0}$ |
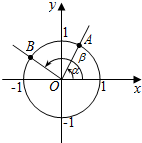 在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.
在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$. 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题: