题目内容
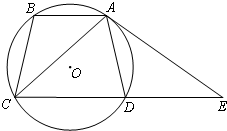 如图,等腰梯形ABCD内接于⊙O,AB∥CD.过点A作⊙O的切线交CD的延长线于点E.求证:∠DAE=∠BAC.
如图,等腰梯形ABCD内接于⊙O,AB∥CD.过点A作⊙O的切线交CD的延长线于点E.求证:∠DAE=∠BAC.考点:弦切角,与圆有关的比例线段
专题:直线与圆
分析:由已知条件推导出AD=BC,从而得到∠ACD=∠BAC.再由AE为圆的切线,能证明∠DAE=∠BAC.
解答:
证明:∵ABCD是等腰梯形,AB∥CD,∴AD=BC.
∴∠ACD=∠BAC.…(4分)
∵AE为圆的切线,∴∠EAD=∠ACD.…(8分)
∴∠DAE=∠BAC.…(10分)
∴∠ACD=∠BAC.…(4分)
∵AE为圆的切线,∴∠EAD=∠ACD.…(8分)
∴∠DAE=∠BAC.…(10分)
点评:本题考查两角相等的证明,是中档题,解题时要认真审题,注意圆的切线的性质的灵活运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
已知锐角三角形的边长分别是3,5,x,则x的取值范围是( )
A、1<x<
| ||
B、4<x<
| ||
| C、1<x<4 | ||
D、4<x<
|
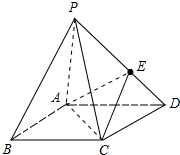 如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.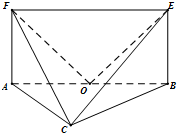 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.