题目内容
 如图,长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a.
如图,长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a.(1)求证:平面AB1D1∥平面C1BD;
(2)求两平面AB1D1与C1BD之间的距离.
(注:两平行平面之间的距离是其中一个平面上任意一点到另一个平面的距离)
考点:点、线、面间的距离计算,平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已知条件推导出BB1D1D是平行四边形,BD∥B1D1,从而得到B1D1∥平面C1BD,同理AD1∥平面C1BD,由此能证明平面AB1D1∥平面C1BD.
(2)法一:连接B1D,得三棱锥B1-C1BD,设平面AB1D1与C1BD之间的距离为h,由此利用等积法能求出平面AB1D1与C1BD之间的距离.
(2)法二:连接AC、A1C1,设AC∩BD=O、A1C1∩B1D1=O1,连接OO1、C1O,作O1E⊥C1O,垂足为E,由已知条件推导出O1E是平面C1BD与平面AB1D1之间的距离,由此能求出结果.
(2)法一:连接B1D,得三棱锥B1-C1BD,设平面AB1D1与C1BD之间的距离为h,由此利用等积法能求出平面AB1D1与C1BD之间的距离.
(2)法二:连接AC、A1C1,设AC∩BD=O、A1C1∩B1D1=O1,连接OO1、C1O,作O1E⊥C1O,垂足为E,由已知条件推导出O1E是平面C1BD与平面AB1D1之间的距离,由此能求出结果.
解答:
(1)证明:∵ABCD-A1B1C1D1是长方体,
∴BB1∥AA1∥DD1,BB1=AA1=DD1…(1分)
∴BB1D1D是平行四边形,BD∥B1D1…(2分)
又B1D1?平面C1BD,BD?平面C1BD,∴B1D1∥平面C1BD…(4分)
同理AD1∥平面C1BD…(5分)
又AD1∩B1D1=D1,∴平面AB1D1∥平面C1BD…(6分)
(2)解法一:连接B1D,得三棱锥B1-C1BD,设平面AB1D1与C1BD之间的距离为h,
依题意,VB1-C1BD=
×S△C1BD×h…(7分)
VB1-C1BD=VD-BB1C1=
×S△BB1C1×CD=
×
×BB1×B1C1×CD=
a3…(9分)
连接AC,设AC∩BD=O,连接C1O,则BO=DO=
a…(10分)
BC1=DC1=
a…(11分)
从而C1O⊥BD,且C1O=
=
a…(12分)
×
×BD×C1O×h=
a3,即
×
×
a×
a×h=
a3…(13分)
解得h=
a,∴平面AB1D1与C1BD之间的距离为
a…(14分)
(2)解法二:连接AC、A1C1,设AC∩BD=O、A1C1∩B1D1=O1,
连接OO1、C1O,作O1E⊥C1O,垂足为E…(7分)
依题意,A1A⊥平面ABCD,所以A1A⊥BD…(8分)
ABCD-A1B1C1D1是长方体,AB=BC,
∴AC⊥BD,A1A∩AC=A,∴BD⊥平面ACC1A1…(9分)
∵BD?平面C1BD,∴平面C1BD⊥平面ACC1A1…(10分)
∵O1E⊥平面C1BD,∴O1E是平面C1BD与平面AB1D1之间的距离…(11分)
在△OO1C1中,OO1=AA1=2a,O1C1=
a…(12分)
OO1⊥平面A1B1C1D1,∠OO1C1=900,OC1=
=
a…(13分)
∴所求距离O1E=
=
a…(14分).
∴BB1∥AA1∥DD1,BB1=AA1=DD1…(1分)
∴BB1D1D是平行四边形,BD∥B1D1…(2分)
又B1D1?平面C1BD,BD?平面C1BD,∴B1D1∥平面C1BD…(4分)
同理AD1∥平面C1BD…(5分)
又AD1∩B1D1=D1,∴平面AB1D1∥平面C1BD…(6分)
(2)解法一:连接B1D,得三棱锥B1-C1BD,设平面AB1D1与C1BD之间的距离为h,
依题意,VB1-C1BD=
| 1 |
| 3 |
VB1-C1BD=VD-BB1C1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
连接AC,设AC∩BD=O,连接C1O,则BO=DO=
| ||
| 2 |
BC1=DC1=
| 5 |
从而C1O⊥BD,且C1O=
| BC12-BO2 |
3
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
| 1 |
| 3 |
解得h=
| 2 |
| 3 |
| 2 |
| 3 |
(2)解法二:连接AC、A1C1,设AC∩BD=O、A1C1∩B1D1=O1,
连接OO1、C1O,作O1E⊥C1O,垂足为E…(7分)
依题意,A1A⊥平面ABCD,所以A1A⊥BD…(8分)
ABCD-A1B1C1D1是长方体,AB=BC,
∴AC⊥BD,A1A∩AC=A,∴BD⊥平面ACC1A1…(9分)
∵BD?平面C1BD,∴平面C1BD⊥平面ACC1A1…(10分)
∵O1E⊥平面C1BD,∴O1E是平面C1BD与平面AB1D1之间的距离…(11分)
在△OO1C1中,OO1=AA1=2a,O1C1=
| ||
| 2 |
OO1⊥平面A1B1C1D1,∠OO1C1=900,OC1=
| OO12+O1C12 |
3
| ||
| 2 |
∴所求距离O1E=
| OO1×O1C1 |
| OC1 |
| 2 |
| 3 |
点评:本题考查平面与平面平行的证明,考查两平行平面间距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
以下棱柱中,最多只有一对面互相平行的是( )
| A、三棱柱 | B、四棱柱 |
| C、八棱柱 | D、六棱柱 |
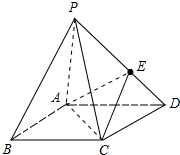 如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
如图,底面是平行四边形的四棱锥P-ABCD,点E在PD上,且PE:ED=2:1,问:在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.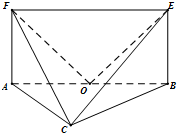 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.