题目内容
关于x的不等式|x-4|+|x-6|≥a恒成立，则a的范围是 ．
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：令f（x）=|x-4|+|x-6|，利用绝对值不等式的性质易求f（x）min=2，利用不等式|x-4|+|x-6|≥a恒成立即可求得答案．
解答：
解：令f（x）=|x-4|+|x-6|，
∵|x-4|+|x-6|≥|（x-4）+（6-x）|=2，
∴f（x）min=2，
又|x-4|+|x-6|≥a恒成立?a≤f（x）min，
∴a≤2．
故答案为：（-∞，2]．
∵|x-4|+|x-6|≥|（x-4）+（6-x）|=2，
∴f（x）min=2，
又|x-4|+|x-6|≥a恒成立?a≤f（x）min，
∴a≤2．
故答案为：（-∞，2]．
点评：本题考查绝对值不等式的解法，考查转化思想与恒成立问题，属于中档题．
练习册系列答案
相关题目
已知点O是以角B为直角顶点的△ABC的外心，且|
|=2，|
|=4，则
•
=（ ）
| AB |
| AC |
| AO |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
函数y=3x+1（x≥-1）的值域是（ ）
| A、（0，+∞） |
| B、（1，+∞） |
| C、[0．+∞） |
| D、[1．+∞） |
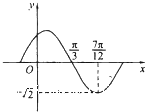函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0）的部分图象如图所示，则Atanφ的值为（ ）A、-
| ||
B、-
| ||
C、
| ||
D、
|