题目内容
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若点P为直线ρcosθ-ρsinθ-4=0上一点,点Q为曲线
(t为参数)上一点,则|PQ|的最小值为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把直线ρcosθ-ρsinθ-4=0化为直角坐标方程x-y-4=0.利用点到直线的距离公式可得:|PQ|=
.再利用二次函数的单调性即可得出最小值.
|t-
| ||
|
解答:
解:由直线ρcosθ-ρsinθ-4=0化为x-y-4=0.
由点到直线的距离公式可得:|PQ|=
=
=
≥
×12=
.
当且仅当t=2时取等号.
∴|PQ|的最小值为
.
故答案为:
.
由点到直线的距离公式可得:|PQ|=
|t-
| ||
|
| ||
| 8 |
| ||
| 8 |
| ||
| 8 |
3
| ||
| 2 |
当且仅当t=2时取等号.
∴|PQ|的最小值为
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
点评:本题考查了把直线的极坐标方程化为直角坐标方程、点到直线的距离公式、二次函数的单调性,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
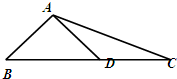 如图,在△ABC中,AD⊥AB,
如图,在△ABC中,AD⊥AB,