题目内容
函数y=3x+1(x≥-1)的值域是( )
| A、(0,+∞) |
| B、(1,+∞) |
| C、[0.+∞) |
| D、[1.+∞) |
考点:函数的值域
专题:函数的性质及应用
分析:考查函数y=3x的单调性,利用x≥-1,求出y的值域.
解答:
解:考查函数y=3x,是定义域上的增函数,
∴当x≥-1时,x+1≥0,
∴3x+1≥30=1,
∴函数y的值域是[1,+∞);
故选:D.
∴当x≥-1时,x+1≥0,
∴3x+1≥30=1,
∴函数y的值域是[1,+∞);
故选:D.
点评:本题考查了利用指数函数的单调性求函数值域的问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=log2[(x-1)(3-x)]的定义域为( )
| A、(1,3) |
| B、[1,3] |
| C、(-∞,1)∪(3,+∞) |
| D、{x|x≠1且x≠3} |
为了得到函数y=cos(x-
)的图象,只需把函数y=cosx图象上所有的点( )
| 1 |
| 3 |
A、向左平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向右平行移动
|
sin120°等于( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
定义行列式运算
=a1a4-a2a3.将函数f(x)=
图象向左平移
个单位后,所得函数图象的一条对称轴是( )
|
|
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
下列三数
,log1682,log27124的大小关系是( )
| 3 |
| 2 |
A、
| ||
B、
| ||
C、log27124<
| ||
D、log27124<log1682<
|
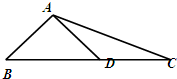 如图,在△ABC中,AD⊥AB,
如图,在△ABC中,AD⊥AB,