题目内容
已知点O是以角B为直角顶点的△ABC的外心，且|
|=2，|
|=4，则
•
=（ ）
| AB |
| AC |
| AO |
| BC |
| A、2 | ||
| B、4 | ||
| C、6 | ||
D、2
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题设条件能推导出O是AC的中点，∠ABC=90°，|
|=|
|=|
|=2，由此能求出|
|和cos＜
，
＞，再由向量的数量积公式能求出结果．
| AO |
| OC |
| AB |
| BC |
| AO |
| BC |
解答：
解：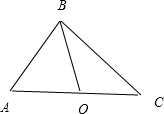
如图，∵点O是以角B为直角顶点的△ABC的外心，
∴O是AC的中点，∠ABC=90°，
∵|
|=2，|
|=4，
∴|
|=|
|=|
|=2，
∴|
|=
=2
，
∴cos＜
，
＞=cos＜
，
＞=
=
=
，
∴
•
=|
|•|
|•cos＜
，
＞
=2×2
×
=6．
故选：C．
如图，∵点O是以角B为直角顶点的△ABC的外心，∴O是AC的中点，∠ABC=90°，
∵|
| AB |
| AC |
∴|
| AO |
| OC |
| AB |
∴|
| BC |
| 42-22 |
| 3 |
∴cos＜
| AO |
| BC |
| CA |
| CB |
|
| ||
| |AC| |
2
| ||
| 4 |
| ||
| 2 |
∴
| AO |
| BC |
| AO |
| BC |
| AO |
| BC |
=2×2
| 3 |
| ||
| 2 |
=6．
故选：C．
点评：本题考查平面向量的数量积的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
函数y=log2[（x-1）（3-x）]的定义域为（ ）
| A、（1，3） |
| B、[1，3] |
| C、（-∞，1）∪（3，+∞） |
| D、{x|x≠1且x≠3} |
sin120°等于（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
下列运算正确的是（ ）
A、（-
| ||||
| B、（x3+1）′=3x2+1 | ||||
| C、（cosx）′=sinx | ||||
D、（log2x）′=
|