题目内容
已知双曲线
-
=1的离心率为2,焦点与椭圆
+
=1的焦点相同,那么双曲线的方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 9 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:求出椭圆椭圆
+
=1的焦点,从而得到双曲线
-
=1的焦点,再由双曲线
-
=1的离心率能求出双曲线的方程.
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:∵椭圆
+
=1的焦点为F1(-4,0),F2(4,0),
∴所求双曲线
-
=1的焦点坐标为F1(-4,0),F2(4,0),
∵双曲线
-
=1的离心率为2,
∴
=
=2,解得a=2,b=
=2
,
∴双曲线方程为
-
=1.
故答案为:
-
=1.
| x2 |
| 25 |
| y2 |
| 9 |
∴所求双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴
| c |
| a |
| 4 |
| a |
| 42-22 |
| 3 |
∴双曲线方程为
| x2 |
| 4 |
| y2 |
| 12 |
故答案为:
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,要熟练掌握双曲线、椭圆的简单性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=log2[(x-1)(3-x)]的定义域为( )
| A、(1,3) |
| B、[1,3] |
| C、(-∞,1)∪(3,+∞) |
| D、{x|x≠1且x≠3} |
定义行列式运算
=a1a4-a2a3.将函数f(x)=
图象向左平移
个单位后,所得函数图象的一条对称轴是( )
|
|
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
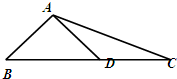 如图,在△ABC中,AD⊥AB,
如图,在△ABC中,AD⊥AB,