Question

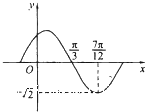函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0）的部分图象如图所示，则Atanφ的值为（　　）

• A、-

  6

• B、-

  3

• C、

  3

• D、

  6

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：由函数的图象直接得到A的值和函数f（x）=Asin（ωx+φ）的四分之一周期，然后求出ω的值，结合五点作图的第三个点列式求出φ，代入Atanφ得答案．

解答： 解：由图象可知，A=

2

，

T

4

=

7π

12

-

π

3

=

π

4

，∴T=π，
再由

2π

ω

=π，得ω=2．
由五点作图可知，ω×

π

3

+φ=π，即2×

π

3

+φ=π，解得：φ=

π

3

．
∴Atanφ=

2

tan

π

3

=

2

×

3

=

6

．
故选：D．

点评：本题考查了由三角函数的图象求三角函数的解析式，训练了利用五点作图法中的特殊点求初相，是中档题．