题目内容
 给出以下判断:
给出以下判断:①已知定点A(-5,0),B(5,0)和动点C,且满足AC,BC所在直线斜率之积为2,则动点C连同点A,B的轨迹为双曲线;
②已知圆C1:(x-4)2+y2=169,圆C2:(x+4)2+y2=9,有一动圆在圆C1的内部且和圆C1内切,和圆C2相外切,则动圆圆心的轨迹为椭圆;
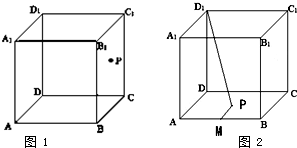
③已知正方体ABCD-A1B1C1D1中(如图1),P是侧面BB1C1C内的动点,若P到直线BC和直线C1D1的距离相等,则动点P的轨迹是线段;
④已知正方体ABCD-A1B1C1D1中(如图2),M为AB中点,棱长为2,P是底面ABCD上的动点,且满足条件PD1=
3PM,则动点P在底面ABCD上形成的轨迹是圆.其中正确命题的序号是
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①根据斜率的计算公式和双曲线的标准方程即可得出;
②利用两圆相内切和外切的性质、椭圆的定义即可得出;
③利用抛物线的定义即可得出;
④设点P(x,y),由于满足条件PD1=3PM,利用两点间的距离公式即可得出.
②利用两圆相内切和外切的性质、椭圆的定义即可得出;
③利用抛物线的定义即可得出;
④设点P(x,y),由于满足条件PD1=3PM,利用两点间的距离公式即可得出.
解答:
解:①设动点C(x,y),由题意可得kACkBC=2,∴
•
=2(x≠±5),
化为
-
=1(x≠±5).因此动点C连同点A,B的轨迹为双曲线
-
=1,正确;
②设动圆的圆心为C(x,y),半径为R,由题意可得:|CC1|=R+3,|CC2|=13-R,
∴|CC1|+|CC2|=16>|C1C2|=8,因此动圆圆心的轨迹为椭圆,正确;
③点P到直线C1D1的距离即点P到点C1的距离,在平面BCC1B1内,到定点C1与到定直线BC的距离相等(定点不在定直线上),则动点P的轨迹是抛物线的一部分,因此不正确;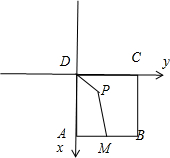
④设点P(x,y),x,y∈[0,2],
∵满足条件PD1=3PM,∴
=3|PM|,
∴22+x2+y2=9[(x-2)2+(y-1)2],化为(x-
)2+(y-
)2=
,
∵x,y∈[0,2],
则动点P在底面ABCD上形成的轨迹是圆的一部分,因此不正确.
综上可知:只有①②正确.
故答案为:①②.
| y |
| x+5 |
| y |
| x-5 |
化为
| x2 |
| 25 |
| y2 |
| 50 |
| x2 |
| 25 |
| y2 |
| 50 |
②设动圆的圆心为C(x,y),半径为R,由题意可得:|CC1|=R+3,|CC2|=13-R,
∴|CC1|+|CC2|=16>|C1C2|=8,因此动圆圆心的轨迹为椭圆,正确;
③点P到直线C1D1的距离即点P到点C1的距离,在平面BCC1B1内,到定点C1与到定直线BC的距离相等(定点不在定直线上),则动点P的轨迹是抛物线的一部分,因此不正确;

④设点P(x,y),x,y∈[0,2],
∵满足条件PD1=3PM,∴
| |DD1|2+|DP|2 |
∴22+x2+y2=9[(x-2)2+(y-1)2],化为(x-
| 9 |
| 4 |
| 9 |
| 8 |
| 77 |
| 64 |
∵x,y∈[0,2],
则动点P在底面ABCD上形成的轨迹是圆的一部分,因此不正确.
综上可知:只有①②正确.
故答案为:①②.
点评:本题综合考查了斜率的计算公式、双曲线的标准方程、两圆相内切和外切的性质、椭圆的定义、抛物线的定义、两点间的距离公式、圆的标准方程等基础知识与基本技能方法,考查了分析问题和解决问题的能力,属于难题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
设实数x、y满足
,则z=max{2x+3y-1,x+2y+2}的取值范围是( )
|
| A、[2,5] |
| B、[2,9] |
| C、[5,9] |
| D、[-1,9] |
 某篮球运动员在5场比赛中得分的茎叶图如图所示,则这位球员得分的平均数等于
某篮球运动员在5场比赛中得分的茎叶图如图所示,则这位球员得分的平均数等于