题目内容
某同学完成一项任务共用去9h，他记录的完成工作量的百分数如下表：
（1）如果用T（x）表示x（h）后他完成工作量的百分数，那么T（5）是多少？求出T（x），并画出其图象；
（2）如果该同学在早晨8时开始工作，什么时候他在休息？
| 时间/h | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 完成的百分数/% | 15 | 30 | 45 | 60 | 60 | 70 | 80 | 90 | 100 |
（2）如果该同学在早晨8时开始工作，什么时候他在休息？
考点：函数解析式的求解及常用方法,函数的图象
专题：函数的性质及应用
分析：（1）由已知中的表格易得T（5），并分析出T（x）为一个分段函数，求出函数解析式后，可画出函数的图象；
（2）由（1）中函数的图象，可得该同学在开始4小时后，开始休息，休息了一个小时，进而得到答案．
（2）由（1）中函数的图象，可得该同学在开始4小时后，开始休息，休息了一个小时，进而得到答案．
解答：
解：（1）由已知中的图表可得：
当h=5时，完成了工作量的60%，
故T（5）=60；
T（x）为一个分段函数，其解析式为：
T（x）=
，
其图象如下图所示：
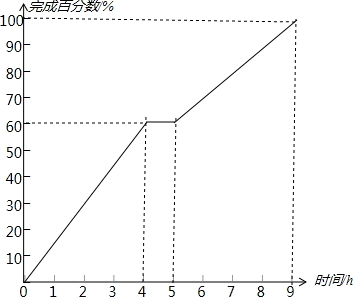
（2）由（1）中函数的图象，可得该同学在开始4小时后，开始休息，休息了一个小时
若该同学在早晨8时开始工作，
则该同学在12点～13点之间休息．
当h=5时，完成了工作量的60%，
故T（5）=60；
T（x）为一个分段函数，其解析式为：
T（x）=
|
其图象如下图所示：
（2）由（1）中函数的图象，可得该同学在开始4小时后，开始休息，休息了一个小时
若该同学在早晨8时开始工作，
则该同学在12点～13点之间休息．
点评：本题考查的知识点是函数解析式的求法，函数的图象，是函数图象和性质的简单综合应用，难度不大，属于基础题．
练习册系列答案
相关题目
已知双曲线C1：
-
=1（a＞0，b＞0）的焦距是实轴长的2倍．若抛物线C2：x2=2py（p＞0）的焦点到双曲线C1的渐近线的距离为2，则抛物线C2的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、x2=
| ||||
B、x2=
| ||||
| C、x2=8y | ||||
| D、x2=16y |
如图，在四棱锥P-ABCD中，AB∥CD，△PAB和△PAD是两个边长为2的正三角形．DC=4，PD⊥PB，点E是CD的中点．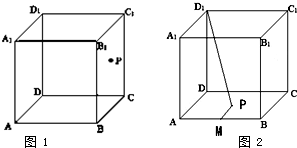
给出以下判断：