题目内容
曲线f（x）=ex在x=0处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到在x=0处的导数值，再求出f（0），然后直接写出切线方程的斜截式．
解答：
解：由f（x）=ex，得f′（x）=ex，
∴f′（0）=e0=1，即曲线f（x）=ex在x=0处的切线的斜率等于1，
又f（0）=1，
∴曲线f（x）=ex在x=0处的切线方程为y=x+1，即x-y+1=0．
故答案为：x-y+1=0．
∴f′（0）=e0=1，即曲线f（x）=ex在x=0处的切线的斜率等于1，
又f（0）=1，
∴曲线f（x）=ex在x=0处的切线方程为y=x+1，即x-y+1=0．
故答案为：x-y+1=0．
点评：本题考查利用导数研究曲线上某点的切线方程，曲线上某点处的导数值，就是曲线在该点处的切线的斜率，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知双曲线C1：
-
=1（a＞0，b＞0）的焦距是实轴长的2倍．若抛物线C2：x2=2py（p＞0）的焦点到双曲线C1的渐近线的距离为2，则抛物线C2的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、x2=
| ||||
B、x2=
| ||||
| C、x2=8y | ||||
| D、x2=16y |
如图，在四棱锥P-ABCD中，AB∥CD，△PAB和△PAD是两个边长为2的正三角形．DC=4，PD⊥PB，点E是CD的中点．
已知ABCD-A1B1C1D1是边长为3的正方体，点P、Q、R分别是棱AB、AD、AA1上的点，AP=AQ=AR=1，则四面体C1PQR的体积为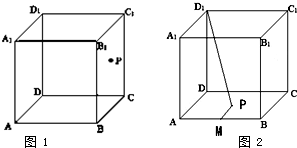
给出以下判断：