题目内容
下列命题中:①、若m>0,则方程x2-x+m=0有实根. ②、若x>1,y>1,则x+y>2的逆命题. ③、对任意的x∈{x|-2<x<4},|x-2|<3的否定形式. ④、△>0是一元二次方程ax2+bx+c=0有一正根和一负根的充要条件.是真命题的有 .
考点:命题的真假判断与应用
专题:简易逻辑
分析:①首先,求解使得方程x2-x+m=0有实根的充要条件,则满足△≥0;然后,求出实数m的范围;
②首先,写出给定命题的逆命题,然后,判断该命题的真假;
③给定的命题为全称命题,写出该命题的否定形式,然后,判断真假;
④根据方程有一正根和一负根,则满足
,然后,给出判断.
②首先,写出给定命题的逆命题,然后,判断该命题的真假;
③给定的命题为全称命题,写出该命题的否定形式,然后,判断真假;
④根据方程有一正根和一负根,则满足
|
解答:
解:对于①:方程x2-x+m=0有实根,
∴△=1-4m≥0,
∴m≤
,
∴该命题是假命题;
对于②:该命题的逆命题为:
若x+y>2,则x>1,y>1.
举反例:取x=-3,y=8,满足x+y>2,
但是推不出x>1,y>1.
∴该命题是假命题;
对于③:对任意的x∈{x|-2<x<4},|x-2|<3的否定形式为:
存在x∈{x|-2<x<4},|x-2|≥3,
∵-2<x<4,
∴-4<x-2<2,∴|x-2|<4,
∴存在这样的x,满足条件,故③为真命题;
对于④:若方程有一正根和一负根,则满足
,
∴该命题是假命题;
故答案为③.
∴△=1-4m≥0,
∴m≤
| 1 |
| 4 |
∴该命题是假命题;
对于②:该命题的逆命题为:
若x+y>2,则x>1,y>1.
举反例:取x=-3,y=8,满足x+y>2,
但是推不出x>1,y>1.
∴该命题是假命题;
对于③:对任意的x∈{x|-2<x<4},|x-2|<3的否定形式为:
存在x∈{x|-2<x<4},|x-2|≥3,
∵-2<x<4,
∴-4<x-2<2,∴|x-2|<4,
∴存在这样的x,满足条件,故③为真命题;
对于④:若方程有一正根和一负根,则满足
|
∴该命题是假命题;
故答案为③.
点评:本题重点考查命题的真假判断,注意全称命题和特称命题的判断方法,属于综合性题目,难度中档.

练习册系列答案
相关题目
已知实数x,y满足不等式组
,且z=x-y的最小值为-3,则实数m的值为( )
|
| A、-1 | ||
B、-
| ||
| C、6 | ||
| D、7 |
“函数f(x)=logax在(0,+∞)上是增函数”是“函数g(x)=x2+2ax+1在(1,+∞)上是增函数”的( )
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E是CD的中点.
如图,在四棱锥P-ABCD中,AB∥CD,△PAB和△PAD是两个边长为2的正三角形.DC=4,PD⊥PB,点E是CD的中点. 已知ABCD-A1B1C1D1是边长为3的正方体,点P、Q、R分别是棱AB、AD、AA1上的点,AP=AQ=AR=1,则四面体C1PQR的体积为
已知ABCD-A1B1C1D1是边长为3的正方体,点P、Q、R分别是棱AB、AD、AA1上的点,AP=AQ=AR=1,则四面体C1PQR的体积为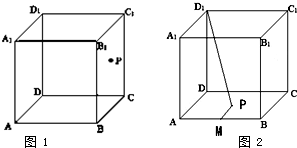 给出以下判断:
给出以下判断: