题目内容
甲、乙、丙三个车床加工的零件分别为350个,700个,1050个,现用分层抽样的方法随机抽取6个零件进行检验.
(Ⅰ)求从甲、乙、丙三个车床中抽取的零件的件数;
(Ⅱ)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求其中至少有一个是乙车床加工的概率.
(Ⅰ)求从甲、乙、丙三个车床中抽取的零件的件数;
(Ⅱ)从抽取的6个零件中任意取出2个,已知这两个零件都不是甲车床加工的,求其中至少有一个是乙车床加工的概率.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(Ⅰ)根据分层抽样的定义即可求出求从甲、乙、丙三个车床中抽取的零件的件数;
(Ⅱ)根据古典概率的概率公式即可求出相应的概率公式.
(Ⅱ)根据古典概率的概率公式即可求出相应的概率公式.
解答:
解:(Ⅰ)由抽样方法可知,
从甲、乙、丙三个车床抽取的零件数分别为1,2,3.
(Ⅱ)即抽取的6个零件为a1,b1,b2,c1,c2,c3.
事件“已知这两个零件都不是甲车床加工点”的可能结果为
(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),
(c1,c2),(c1,c3),(c2,c3),共10种可能;
事件“其中至少有一个是乙车床加工的”的可能结果为
(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),
共7种可能.
故所求概率为P=0.7.
从甲、乙、丙三个车床抽取的零件数分别为1,2,3.
(Ⅱ)即抽取的6个零件为a1,b1,b2,c1,c2,c3.
事件“已知这两个零件都不是甲车床加工点”的可能结果为
(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),
(c1,c2),(c1,c3),(c2,c3),共10种可能;
事件“其中至少有一个是乙车床加工的”的可能结果为
(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),
共7种可能.
故所求概率为P=0.7.
点评:本题主要考查分层抽样的定义和应用,以及古典概率的概率公式的计算,要求熟练掌握概率的概率公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法错误的是( )
| A、如果直线上的两点在一个平面内,那么此直线在平面内 |
| B、过空间中三点,有且只有一个平面 |
| C、若两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
| D、平行于同一条直线的两条直线互相平行 |
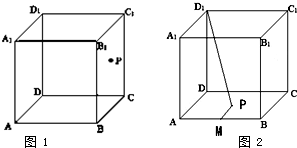 给出以下判断:
给出以下判断: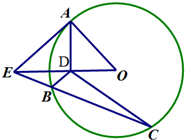 如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.
如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.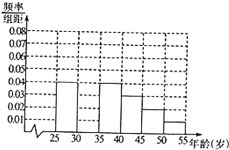 某同学在寒假期间进行社会实践活动,对[25,55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查,若生活习惯符合环保观念的称为“环保族”,否则称为“非环保族”,得到如下统计表和各年龄段人数的频率分布直方图:
某同学在寒假期间进行社会实践活动,对[25,55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查,若生活习惯符合环保观念的称为“环保族”,否则称为“非环保族”,得到如下统计表和各年龄段人数的频率分布直方图: