题目内容
函数f(x)=xex-ex+1的单调递增区间是( )
| A、(-∞,e) |
| B、(1,e) |
| C、(e,+∞) |
| D、(e-1,+∞) |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求函数的导数,解f′(x)≥0,即可求出函数的单调递增区间.
解答:
解:∵函数y=xex-ex+1=(x-e)ex,
∴f′(x)=ex+(x-e)ex,
由f′(x)≥0得ex(1+x)≥ex+1,
即x≥e-1,
即函数的单调增区间为(e-1,+∞)
故选:D.
∴f′(x)=ex+(x-e)ex,
由f′(x)≥0得ex(1+x)≥ex+1,
即x≥e-1,
即函数的单调增区间为(e-1,+∞)
故选:D.
点评:本题主要考查函数单调性和单调区间的求解,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
从5名学生中选出4名分别参加A,B,C,D四科竞赛,其中甲不能参加A,B两科竞赛,则不同的参赛方案种数为( )
| A、24 | B、48 | C、72 | D、120 |
函数y=x3-3x+1在x0处取极大值y0,而函数y=ax-1过点(x0,y0),则函数y=|ax-1|的增区间为( )
| A、(-∞,+∞) |
| B、(-∞,0) |
| C、(-∞,1) |
| D、(0,+∞) |
已知函数f(x)=
,若|f(x)|≥kx,则k的取值范围是( )
|
| A、(-∞,0] |
| B、(-∞,1] |
| C、[-2,1] |
| D、[-2,0] |
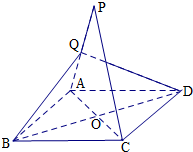 如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.
如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.