题目内容
已知圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为
(t为参数,t∈R).
(Ⅰ)求直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)求直线l与圆C相交的弦长.
|
(Ⅰ)求直线l的普通方程和圆C的直角坐标方程;
(Ⅱ)求直线l与圆C相交的弦长.
考点:参数方程化成普通方程,直线与圆的位置关系
专题:选作题,坐标系和参数方程
分析:(Ⅰ)利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得圆的直角坐标方程;
(Ⅱ)利用点到直线的距离公式求出圆心C到直线l的距离d,由垂径定理及勾股定理即可求出弦长|AB|.
(Ⅱ)利用点到直线的距离公式求出圆心C到直线l的距离d,由垂径定理及勾股定理即可求出弦长|AB|.
解答:
解:(Ⅰ)由ρ=2cosθ⇒ρ2=2ρcosθ⇒x2+y2-2x=0⇒(x-1)2+y2=1,
直线l的参数方程为
(t为参数,t∈R)的普通方程为x-y-2=0;
(Ⅱ)圆心到直线距离为:d=
=
.
∴弦长|AB|=2
=
.
直线l的参数方程为
|
(Ⅱ)圆心到直线距离为:d=
| |1-0-2| | ||
|
| ||
| 2 |
∴弦长|AB|=2
1-
|
| 2 |
点评:本题考查了直线的参数方程、简单曲线的极坐标方程和直线与圆的位置关系等知识点,属于中档题.

练习册系列答案
相关题目
函数f(x)=xex-ex+1的单调递增区间是( )
| A、(-∞,e) |
| B、(1,e) |
| C、(e,+∞) |
| D、(e-1,+∞) |
表示满足(x-y)(x+2y-2)≥0的点(x,y)所在的区域应为( )
A、 |
B、 |
C、 |
D、 |
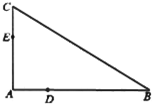 如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.