题目内容
已知函数f(x)=|x-1|+|2-x|.
(Ⅰ)解不等式f(x)>2
(Ⅱ)若f(x)≥|a-1|恒成立,求实数a的范围.
(Ⅰ)解不等式f(x)>2
(Ⅱ)若f(x)≥|a-1|恒成立,求实数a的范围.
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)对x分段去绝对值求解不等式f(x)>2,取并集得答案;
(Ⅱ)由绝对值的几何意义求出f(x)的最小值,然后求解关于a的绝对值的不等式得答案.
(Ⅱ)由绝对值的几何意义求出f(x)的最小值,然后求解关于a的绝对值的不等式得答案.
解答:
解:(Ⅰ)由不等式f(x)>2,得|x-1|+|2-x|>2,
当x<1时,化为-x+1+2-x>2,即x<
;
当1≤x≤2时,化为x-1+2-x>2,此式显然不成立;
当x>2时,化为x-1-2+x>2,即x>
.
∴不等式f(x)>2的解集为(-∞,
)∪(
,+∞);
(Ⅱ)f(x)≥|a-1|恒成立,即
|x-1|+|2-x|≥|a-1|恒成立,
由绝对值的几何意义得|x-1|+|2-x|≥2,
∴|a-1|≤2,解得-1≤a≤3.
∴使f(x)≥|a-1|恒成立的实数a的范围是[-1,3].
当x<1时,化为-x+1+2-x>2,即x<
| 1 |
| 2 |
当1≤x≤2时,化为x-1+2-x>2,此式显然不成立;
当x>2时,化为x-1-2+x>2,即x>
| 5 |
| 2 |
∴不等式f(x)>2的解集为(-∞,
| 1 |
| 2 |
| 5 |
| 2 |
(Ⅱ)f(x)≥|a-1|恒成立,即
|x-1|+|2-x|≥|a-1|恒成立,
由绝对值的几何意义得|x-1|+|2-x|≥2,
∴|a-1|≤2,解得-1≤a≤3.
∴使f(x)≥|a-1|恒成立的实数a的范围是[-1,3].
点评:本题考查了绝对值不等式的解法,考查了绝对值的几何意义,体现了数学转化思想方法,是中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
直线l:y=
x经过曲线C:y=
sinωx(ω>0)在区间[0,+∞)上的第一个最高点,则曲线C的最小正周期是( )
| 3 |
| 3 |
| A、4π | B、2π | C、4 | D、2 |
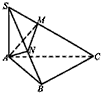 如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.
如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC. 如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.若AD=AB=2,则EB=
如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.若AD=AB=2,则EB=