题目内容
若不等式-1≤sin2x+4cosx+a2≤13对一切实数x均成立,则实数a的取值范围是 .
考点:三角函数的最值
专题:三角函数的图像与性质
分析:首先,根据题意,换元法得到关于t的二次函数,然后利用函数的单调性求解函数y=-t2+4t+1+a2的最大值和最小值,然后,根据不等式-1≤sin2x+4cosx+a2≤13对一切实数x均成立,等价于
,求解实数a的取值范围.
|
解答:
解:设函数y=sin2x+4cosx+a2,
=1-cos2x+4cosx+a2
=-cos2x+4cosx+1+a2
令cosx=t,则t∈[-1,1],
∴y=-t2+4t+1+a2
=-(t+2)2+a2
在区间[-1,1]上为减函数,
∴当t=-1时,函数y取得最大值a2-4,
当t=1时,函数y取得最小值4+a2,
∵不等式-1≤sin2x+4cosx+a2≤13对一切实数x均成立,
∴
,
∴-
≤a≤
,
故答案为:[-
,
].
=1-cos2x+4cosx+a2
=-cos2x+4cosx+1+a2
令cosx=t,则t∈[-1,1],
∴y=-t2+4t+1+a2
=-(t+2)2+a2
在区间[-1,1]上为减函数,
∴当t=-1时,函数y取得最大值a2-4,
当t=1时,函数y取得最小值4+a2,
∵不等式-1≤sin2x+4cosx+a2≤13对一切实数x均成立,
∴
|
∴-
| 17 |
| 17 |
故答案为:[-
| 17 |
| 17 |
点评:本题重点考查了不等式的恒成立问题,函数的最值等知识,属于中档题.解题的关键是熟练掌握二次函数的图象与性质.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
下列命题错误的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1” |
| B、若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 |
| C、△ABC中,sinA>sinB是A>B的充要条件 |
| D、若p∨q为真命题,则p、q均为真命题 |
 如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、是CC1的中点,求证:PB∥面AD1C.(用两种方法)
如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、是CC1的中点,求证:PB∥面AD1C.(用两种方法)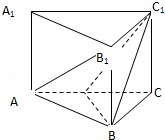 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.
已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.