题目内容
18．若复数$\frac{4+bi}{1+i}$（b∈R）的实部与虚部互为相反数，则b=0．分析 利用复数代数形式的乘除运算化简，再由实部与虚部的和为0求得b值．
解答 解：∵$\frac{4+bi}{1+i}$=$\frac{（4+bi）（1-i）}{（1+i）（1-i）}=\frac{（4+b）+（b-4）i}{2}$，
又复数$\frac{4+bi}{1+i}$的实部与虚部互为相反数，
∴4+b+b-4=0，即b=0．
故答案为：0．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础的计算题．
练习册系列答案
优生乐园系列答案
相关题目
8．若复数z满足关系$z•\overline{z}$=1，则z对应的复平面的点的轨迹是（ ）
| A． | 圆 | B． | 椭圆 | C． | 双曲线 | D． | 直线 |
10．
已知函数f（x）的定义域为R，f（-1）=f（2）=1，其导数f′（x）的图象如图所示，设实数x，y满足$\left\{\begin{array}{l}{xy≥0}\\{f（2x+y）≤1}\end{array}\right.$则表达式z=3x+y的最小值为（ ）
已知函数f（x）的定义域为R，f（-1）=f（2）=1，其导数f′（x）的图象如图所示，设实数x，y满足$\left\{\begin{array}{l}{xy≥0}\\{f（2x+y）≤1}\end{array}\right.$则表达式z=3x+y的最小值为（ ）| A． | 0 | B． | -1 | C． | -$\frac{3}{2}$ | D． | -3 |
7．
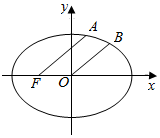如图，已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1，F是其左焦点，A、B在椭圆上，满足FA∥OB且|FA|：|OB|=3：2，则点A的横坐标为（ ）
如图，已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1，F是其左焦点，A、B在椭圆上，满足FA∥OB且|FA|：|OB|=3：2，则点A的横坐标为（ ）| A． | 1 | B． | $\frac{3}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |