题目内容
6．已知函数f（x）=xlnx+a．（1）若函数y=f（x）在x=e处的切线方程为y=2x，求实数a的值；
（2）设m＞0，当x∈[m，2m]时，求f（x）的最小值；
（3）求证：${?_n}∈{N_+}，{e^{1+\frac{1}{n}}}＞{（1+\frac{1}{n}）^e}$．
分析 （1）求出切点坐标，代入函数进行求解即可．
（2）求好的导数，判断函数的单调性进行求解即可．
（3）令x=$\frac{n}{n+1}$，利用（2）的结论，构造不等式进行证明即可．
解答 解：（1）∵函数y=f（x）在x=e处的切线方程为y=2x，
∴此时y=2e，即切点坐标为（e，2e），
则切点也在函数f（x）上，则f（e）=elne+a=e+a=2e，
则a=e，
（2）函数的导数f′（x）=lnx+1，
由f′（x）＞0得x＞$\frac{1}{e}$，由f′（x）＜0得0＜x＜$\frac{1}{e}$，
即函数在（$\frac{1}{e}$，+∞）上为增函数，在（0，$\frac{1}{e}$）上为减函数，
①当2m≤$\frac{1}{e}$，即m≤$\frac{1}{2e}$时，f（x）min=f（2m）=2mln2m+a，
②当m＜$\frac{1}{e}$＜2m，即$\frac{1}{2e}$＜m＜$\frac{1}{e}$时，f（x）min=f（$\frac{1}{e}$）=-$\frac{1}{e}$+a，
③当m≥$\frac{1}{e}$时，f（x）min=f（m）=mlnm+a．
（3）令x=$\frac{n}{n+1}$，则x＞$\frac{1}{e}$，
由（2）知，xlnx+a≥-$\frac{1}{e}$+a，
即xlnx≥-$\frac{1}{e}$，当x=$\frac{1}{e}$时，取等号，
∴$\frac{n}{n+1}$ln=$\frac{n}{n+1}$＞-$\frac{1}{e}$，则-ln$\frac{n+1}{n}$＞-$\frac{1}{e}$•$\frac{n+1}{n}$，即e•$\frac{n+1}{n}$＜$\frac{n+1}{n}$，即ln（1+$\frac{1}{n}$）e＜1+$\frac{1}{n}$，
∴${?_n}∈{N_+}，{e^{1+\frac{1}{n}}}＞{（1+\frac{1}{n}）^e}$．
点评 本题主要考查导数的综合应用以及利用导数证明不等式，综合性较强，难度较大．
名校课堂系列答案
如图，已知在等腰梯形ABCD中，AB=4，AB∥CD，∠BAD=45°，E，F，G分别是AB，BC，CD的中点，若$\overrightarrow{EF}$在$\overrightarrow{AG}$方向上的投影为$\frac{7}{10}\sqrt{4+\frac{1}{2}A{D^2}}$，则$\frac{{|\overrightarrow{AB}|}}{{|\overrightarrow{CD}|}}$=（ ）
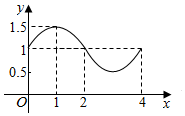函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2013）+f（2014）+f（2015）+f（2016）的值分别为（ ）| A． | f（x）=$\frac{1}{2}$sin2πx+1，S=2016 | B． | f（x）=$\frac{1}{2}$sin2πx+1，S=2016$\frac{1}{2}$ | ||
| C． | f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2017$\frac{1}{2}$ | D． | f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2017 |