题目内容
10. 已知函数f(x)的定义域为R,f(-1)=f(2)=1,其导数f′(x)的图象如图所示,设实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$则表达式z=3x+y的最小值为( )
已知函数f(x)的定义域为R,f(-1)=f(2)=1,其导数f′(x)的图象如图所示,设实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$则表达式z=3x+y的最小值为( )| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
分析 根据导函数的图象,函数先单调递减,后单调递增,绘制出函数大致图象,由方程组写出x、y的取值范围,绘出其区间,根据目标函数求出z的最小值.
解答 解:由导函数的图象可知,函数先单调递减,后单调递增,函数图象如图: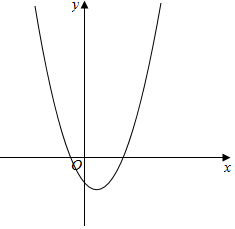
实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$,f(-1)=f(2)=1即$\left\{\begin{array}{l}{xy≥0}\\{2x+y≥-1}\\{2x+y≤2}\end{array}\right.$,所围成的区域如下图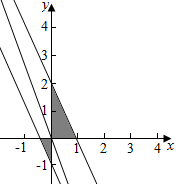
y=-3x+z
∴当经过点(-$\frac{1}{2}$,0)时z=$-\frac{3}{2}$
z的最小值为$-\frac{3}{2}$.
故答案选 C
点评 本题考查会根据导函数的图象绘制函数的大致图象,判断其单调性,利用线性规划求目标函数的最小值,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
20.已知平面直角坐标系中两个定点E(3,2),F(-3,2),如果对于常数λ,在函数y=|x+2|+|x-2|-4,(x∈[-4,4])的图象上有且只有6个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
| A. | (-5,-$\frac{9}{5}$) | B. | (-$\frac{9}{5}$,11) | C. | (-$\frac{9}{5}$,-1) | D. | (-5,11) |
5.已知y=f(x)(x∈R)的导函数为f′(x).若f(x)-f(-x)=2x3,且当x≥0时,f′(x)>3x2,则不等式f(x)-f(x-1)>3x2-3x+1的解集是( )
| A. | $(-\frac{1}{2},+∞)$ | B. | $(\frac{1}{2},+∞)$ | C. | $(-∞,-\frac{1}{2})$ | D. | $(-∞,\frac{1}{2})$ |
2.已知命题p:?x∈R,cosx=$\frac{5}{4}$;命题q:?x∈R,2x+1>0.则下列正确的是( )
| A. | p∧q是真命题 | B. | p∧(﹁q)是真命题 | C. | ﹁p∧q是真命题 | D. | ﹁p∧﹁q是假命题 |