题目内容
9．方程log2（9x+7）=2+log2（3x+1）的解为x=0和x=1．分析 由对数的运算性质化对数方程为关于3x的一元二次方程，求得3x的值，进一步求得x值得答案．
解答 解：由log2（9x+7）=2+log2（3x+1），得
log2（9x+7）=log24（3x+1），
即9x+7=4（3x+1），
化为（3x）2-4•3x+3=0，
解得：3x=1和3x=3，
∴x=0和x=1．
故答案为：x=0和x=1．
点评 本题考查对数方程的解法，体现了数学转化思想方法，是基础题．
练习册系列答案
科学实验活动册系列答案
相关题目
20．已知平面直角坐标系中两个定点E（3，2），F（-3，2），如果对于常数λ，在函数y=|x+2|+|x-2|-4，（x∈[-4，4]）的图象上有且只有6个不同的点P，使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立，那么λ的取值范围是（ ）
| A． | （-5，-$\frac{9}{5}$） | B． | （-$\frac{9}{5}$，11） | C． | （-$\frac{9}{5}$，-1） | D． | （-5，11） |
17．
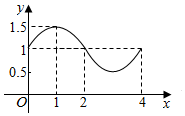函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2013）+f（2014）+f（2015）+f（2016）的值分别为（ ）
函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2013）+f（2014）+f（2015）+f（2016）的值分别为（ ）| A． | f（x）=$\frac{1}{2}$sin2πx+1，S=2016 | B． | f（x）=$\frac{1}{2}$sin2πx+1，S=2016$\frac{1}{2}$ | ||
| C． | f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2017$\frac{1}{2}$ | D． | f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2017 |
4．若函数f（x）=2sin2x的图象向右平移φ（0＜φ＜$\frac{π}{2}$）个单位后得到函数g（x）的图象，若对满足|f（x1）-g（x2）|=4的x1、x2，有|x1-x2|的最小值为$\frac{π}{6}$，则φ=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{12}$ |