题目内容
5.研究函数$f(x)=\frac{{{x^2}+3}}{{{x^2}-4}}$的性质,并作出其图象.分析 根据已知中函数$f(x)=\frac{{{x^2}+3}}{{{x^2}-4}}$的解析式,画出函数的图象,数形结合,可得函数的定义域,奇偶性,单调性等性质.
解答 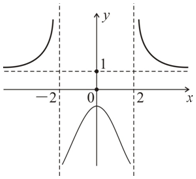 (本小题满分12分)
(本小题满分12分)
解:(1)函数的定义域为{x/x∈R,x≠±2}…(1分)
(2)函数的奇偶性:∵$f(-x)=\frac{{{{({-x})}^2}+3}}{{{{({-x})}^2}-4}}=\frac{{{x^2}+3}}{{{x^2}-4}}=f(x)$
∴f(x)是偶函数…(3分)
(3)∵$f(x)=\frac{{{x^2}+3}}{{{x^2}-4}}=1+\frac{7}{{{x^2}-4}}≠1$,当x∈[0,2)时,$f(x)≤-\frac{3}{4}$且递减;
当x∈(2,+∞)时,f(x)>1,递减且以直线x=2,y=1为渐近线;
又f(x)是偶函数
∴f(x)当x∈(-2,0]时,$f(x)≤-\frac{3}{4}$且递增;
当x∈(-∞,-2)时,f(x)>1,递增且以直线x=-2,y=1为渐近线;…(8分)
(4)函数f(x)的图象如图所示.…(12分)
点评 本题考查的知识点是函数的图象,函数的性质,本题中的函数即为所谓的“囧函数”,要求学生掌握.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
15.已知m>e>n>1>k>0(e为自然数2.7…),且x=m${\;}^{\frac{1}{e}}$,y=lnn,z=logke,则( )
| A. | x>y>z | B. | x>z>y | C. | y>x>z | D. | y>z>x |
13.下列函数中既是偶函数,又在(0,+∞)上单调递减的为( )
| A. | $y={x^{-\frac{1}{2}}}$ | B. | y=x-2 | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x2 |
10.若偶函数f(x)在[1,+∞)上是减函数,则下列关系式中成立的是( )
| A. | $f(2)<f(-\frac{3}{2})<f(-1)$ | B. | $f(-\frac{3}{2})<f(-1)<f(2)$ | C. | $f(2)<f(-1)<f(-\frac{3}{2})$ | D. | $f(-1)<f(-\frac{3}{2})<f(2)$ |
17.程序框图如图所示,当$A=\frac{12}{13}$时,输出的k的值为( )


| A. | 11 | B. | 12 | C. | 13 | D. | 14 |