题目内容
14.有一球内接圆锥,底面圆周和顶点均在球面上,其底面积为4π,已知球的半径R=3,则此圆锥的体积为$\frac{{4({3-\sqrt{5}})π}}{3}$或$\frac{{4({3+\sqrt{5}})π}}{3}$.分析 求出圆锥的高,即可求出圆锥的体积.
解答 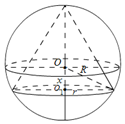 解:由πr2=4π得圆锥底面半径为r=2,如图设OO1=x,
解:由πr2=4π得圆锥底面半径为r=2,如图设OO1=x,
则$x=\sqrt{{R^2}-{r^2}}=\sqrt{{3^2}-{2^2}}=\sqrt{5}$,圆锥的高$h=R+x=3+\sqrt{5}$或$h=R-x=3-\sqrt{5}$
所以,圆锥的体积为$V=\frac{1}{3}Sh=\frac{1}{3}×4π×(3+\sqrt{5})=\frac{{4({3+\sqrt{5}})π}}{3}$
或$V=\frac{1}{3}Sh=\frac{1}{3}×4π×(3-\sqrt{5})=\frac{{4({3-\sqrt{5}})π}}{3}$.
故答案为$\frac{{4({3-\sqrt{5}})π}}{3}$或$\frac{{4({3+\sqrt{5}})π}}{3}$.
点评 本题考查圆锥的体积,考查学生的计算能力,正确求出圆锥的高是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.执行如图的程序框图,则输出的n是( )
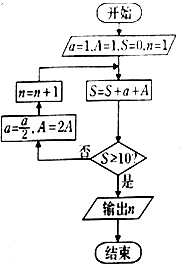

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
2.命题“?x>0,lnx>0”的否定是( )
| A. | ?x>0,lnx>0 | B. | ?x>0,lnx>0 | C. | ?x>0,lnx≥0 | D. | ?x>0,lnx≤0 |