题目内容
15.已知m>e>n>1>k>0(e为自然数2.7…),且x=m${\;}^{\frac{1}{e}}$,y=lnn,z=logke,则( )| A. | x>y>z | B. | x>z>y | C. | y>x>z | D. | y>z>x |
分析 根据对数函数和幂函数的性质,分别比较x,y,z与0,1的关系即可.
解答 解:由m>e>n>1>k>0(e为自然数2.7…),且x=m${\;}^{\frac{1}{e}}$>1,0<y=lnn<1,z=logke<0,
则x>y>z,
故选:A
点评 本题考查了对数函数和幂函数的性质,关键是比较和中间值0,1的关系,属于基础题.

练习册系列答案
相关题目
5.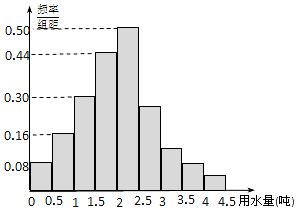 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
(1)根据频率分布直方图估计这组数据的众数与平均数;
(2)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?
 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:| 分组 | 频数 |
| [0,0.5) | 4 |
| [0.5,1) | 8 |
| [1,1.5) | 15 |
| [1.5,2) | 22 |
| [2,2.5) | 25 |
| [2.5,3) | 14 |
| [3,3.5) | 6 |
| [3.5,4) | 4 |
| [4,4.5) | 2 |
| 合计 | 100 |
(2)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?
3.已知lg(x+y)=lgx+lgy,则x+y的取值范围是( )
| A. | (0,1] | B. | [2,+∞) | C. | (0,4] | D. | [4,+∞) |
10.命题P:2016≤2017,则下列关于命题P说法正确的是.( )
| A. | 命题P使用了逻辑联结词“或”,是假命题 | |
| B. | 命题P使用了逻辑联结词“且”,是假命题 | |
| C. | 命题P使用了逻辑联结词“非”,是假命题 | |
| D. | 命题P使用了逻辑联结词“或”,是真命题 |
7.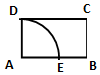 如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )
 如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为距形,AB=$\sqrt{3}$,BC=1,以A为圆心,AD为半径画圆,交线段AB于E,在圆弧DE上任取一点P,则直线AP与线段BC有公共点的概率为( )| A. | $\frac{\sqrt{3}π}{12}$ | B. | $\frac{12-\sqrt{3}π}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
4.执行如图的程序框图,则输出的n是( )
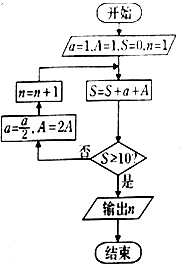

| A. | 5 | B. | 4 | C. | 3 | D. | 2 |