题目内容
17.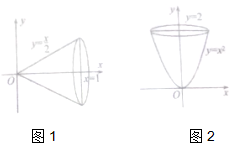 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
分析 根据类比推理,结合定积分的应用,即可求出旋转体的体积.
解答 解:根据类比推理得体积V=${∫}_{0}^{2}π(\sqrt{y})^{2}dy$=$\frac{1}{2}π{y}^{2}{|}_{0}^{2}$=2π,
故选:D.
点评 本题主要考查旋转体的体积的计算,根据类比推理是解决本题的关键.

练习册系列答案
相关题目
8.原点到直线x+2y-5=0的距离为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 2 | D. | $\frac{1}{\sqrt{5}}$ |
5.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f'(x),且有2f(x)+xf'(x)>x2,则不等式(x+2017)2f(x+2017)-4f(-2)>0的解集为( )
| A. | (-∞,-2015) | B. | (-∞,-2019) | C. | (-2015,0) | D. | (-2019,0) |
6.方程$\sqrt{1-{x}^{2}}$=kx+2有两解,则实数k的取值范围是( )
| A. | (-2,-$\sqrt{3}$]∪[$\sqrt{3}$,2) | B. | [-2,-$\sqrt{3}$)∪($\sqrt{3}$,2] | C. | [-2,2] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
7. 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
请你根据频率分布表解答下列问题:
(1)求出频率分布表中①、②、③、④、⑤处的值;
(2)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序功能是什么?求输出S的值.
 为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:
为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表:| 序号 (i) | 分组 (分数) | 组中值 (Gi) | 频数 (人数) | 频率 (Fi) |
| 1 | [60,70) | 65 | ① | 0.10 |
| 2 | [70,80) | 75 | 20 | ② |
| 3 | [80,90) | 85 | ③ | 0.20 |
| 4 | [90,100) | 95 | ④ | ⑤ |
| 合计 | 50 | 1 | ||
(1)求出频率分布表中①、②、③、④、⑤处的值;
(2)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序功能是什么?求输出S的值.
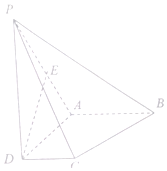 如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.