题目内容
7.德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数$f(x)=\left\{\begin{array}{l}1,x为有理数\\ 0,x为无理数\end{array}\right.$称为狄利克雷函数,关于函数f(x)有以下四个命题:①f(f(x))=1;
②函数f(x)是奇函数
③任意一个非零无理数T,f(x+T)=f(x)对任意x∈R恒成立;
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形.
其中真命题的序号为①④.(写出所有正确命题的序号).
分析 ①根据函数的对应法则,可得不管x是有理数还是无理数,均有f(f(x))=1;
②根据函数奇偶性的定义,可得f(x)是偶函数;
③根据函数的表达式,结合有理数和无理数的性质;
④取x1=-$\frac{\sqrt{3}}{3}$,x2=0,x3=$\frac{\sqrt{3}}{3}$,可得A($\frac{\sqrt{3}}{3}$,0),B(0,1),C(-$\frac{\sqrt{3}}{3}$,0),三点恰好构成等边三角形,即可判断.
解答 解:①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0,
∴当x为有理数时,ff((x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1,
即不管x是有理数还是无理数,均有f(f(x))=1,故①正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有f(-x)=f(x),f(x)为偶函数,故②不正确;
③由于非零无理数T,若x是有理数,则x+T是无理数; 若x是无理数,则x+T不确定,
∴根据函数的表达式,任取一个不为零的无理数T,f(x+T)=f(x)对x∈R不恒成立,故③不正确;
④取x1=-$\frac{\sqrt{3}}{3}$,x2=0,x3=$\frac{\sqrt{3}}{3}$,可得f(x1)=0,f(x2)=1,f(x3)=0,
∴A($\frac{\sqrt{3}}{3}$,0),B(0,1),C(-$\frac{\sqrt{3}}{3}$,0),恰好△ABC为等边三角形,故④正确.
故答案为:①④.
点评 本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在(2x+a)5的展开式中,含x4项的系数等于160,则${∫}_{0}^{a}$(ex+2x)dx等于( )
| A. | e2+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
 如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=$\frac{1}{2}$BE=2,平面BCDE丄平面ABC,又已知△ABC为等腰直角三角形,AB=AC=4,M是BC的中点.
如图,四边形BCDE是直角梯形,CD∥BE,CD丄BC,CD=$\frac{1}{2}$BE=2,平面BCDE丄平面ABC,又已知△ABC为等腰直角三角形,AB=AC=4,M是BC的中点.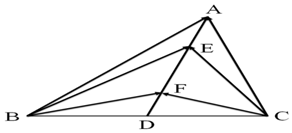 (2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,
(2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,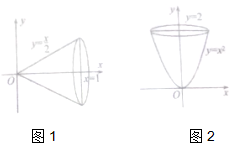 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )