题目内容
6.方程$\sqrt{1-{x}^{2}}$=kx+2有两解,则实数k的取值范围是( )| A. | (-2,-$\sqrt{3}$]∪[$\sqrt{3}$,2) | B. | [-2,-$\sqrt{3}$)∪($\sqrt{3}$,2] | C. | [-2,2] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
分析 将问题转化为两个函数的交点问题,画出函数图象,结合图象,从而求出k的范围.
解答 解:设y=f(x)=$\sqrt{1-{x}^{2}}$,(y≥0,-1≤x≤1);即x2+y2=1 (半圆),
y=h(x)=kx+2 (x∈R) 即y-2=kx,直线恒过点M(0,2),
∵方程f(x)=h(x)有两个不同的实数根,(k>0)即y=f(x)和y=h(x)有两个不同的交点,
画出f(x),h(x)的图象,如图示: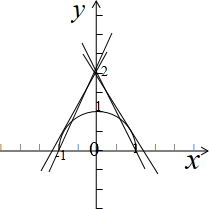 ,
,
当直线与圆相切时,k=±$\sqrt{3}$,
当直线过(0,2),(-1,0)时,k=±2,
∴-2≤k<-$\sqrt{3}$或$\sqrt{3}$<k≤2,
故选B.
点评 本题考查了函数的零点问题,考查了转化思想,是一道中档题.

练习册系列答案
相关题目
17.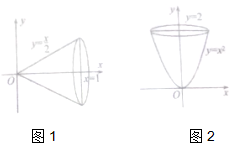 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
15.若?x>0,4a>x2-x3恒成立,则a的取值范围为( )
| A. | $({\frac{1}{27},+∞})$ | B. | $({\frac{4}{27},+∞})$ | C. | $[{\frac{1}{27},+∞})$ | D. | $[{\frac{4}{27},+∞})$ |
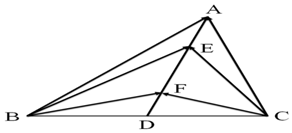 (2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,
(2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,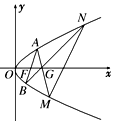 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2). 如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点
如图所示,在所有棱长都为2a的直三棱柱ABC-A1B1C1中,D点为棱AB的中点