题目内容
2.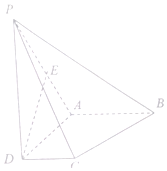 如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.(1)求证:DE⊥PB
(2)求平面PAD和平面PBC所成锐二面角的余弦值.
分析 如图以D为原点建立空间直角坐标系D-xyz,则D(0,0,0),A(0,2,0),B(2,2,0),C(1,0,0),P(0,0,2),E(0,1,1)
(1)可得$\overrightarrow{DE}•\overrightarrow{PB}=0×2+2×1+(-2)×1=0$,DE⊥PB.
(2)求出平面PBC的法向量为$\overrightarrow{m}=(x,y,z)$,可知平面PAD的法向量为$\overrightarrow{DC}=(1,0,0)$.
cos$<\overrightarrow{m},\overrightarrow{DC}>=\frac{\sqrt{6}}{3}$,即可得平面PAD和平面PBC所成锐二面角的余弦值
解答 解:如图以D为原点建立空间直角坐标系D-xyz,
∵四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°
且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点
则D(0,0,0),A(0,2,0),B(2,2,0),
C(1,0,0),P(0,0,2),E(0,1,1)
(1)证明:可得$\overrightarrow{PB}=(2,2,-2),\overrightarrow{DE}=(0,1,1)$,
即$\overrightarrow{DE}•\overrightarrow{PB}=0×2+2×1+(-2)×1=0$,
∴DE⊥PB.
(2)设平面PBC的法向量为$\overrightarrow{m}=(x,y,z)$,
$\overrightarrow{CP}=(-1,0,2),\overrightarrow{CB}=(1,2,0)$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CP}=-x+2z=0}\\{\overrightarrow{m}•\overrightarrow{CB}=x+2y=0}\end{array}\right.$,取$\overrightarrow{m}=(2,-1,1)$.
可知平面PAD的法向量为$\overrightarrow{DC}=(1,0,0)$.
cos$<\overrightarrow{m},\overrightarrow{DC}>=\frac{\sqrt{6}}{3}$,
∴平面PAD和平面PBC所成锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查直线与线垂直的证明,考查平面与平面所成的角的余弦值的求法,解题时要认真审题,注意等价转化思想和向量法的合理运用.属于中档题.

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{2}$](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$]((k∈Z) | D. | [kπ-$\frac{π}{2}$,kπ]((k∈Z) |
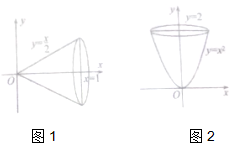 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
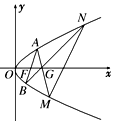 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)任作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).