题目内容
5.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f'(x),且有2f(x)+xf'(x)>x2,则不等式(x+2017)2f(x+2017)-4f(-2)>0的解集为( )| A. | (-∞,-2015) | B. | (-∞,-2019) | C. | (-2015,0) | D. | (-2019,0) |
分析 根据条件,构造函数,利用函数的单调性和导数之间的关系,将不等式进行转化即可得到结论.
解答 解:由2f(x)+xf′(x)>x2,(x<0),
得:2xf(x)+x2f′(x)<x3,
即[x2f(x)]′<x3<0,
令F(x)=x2f(x),
则当x<0时,
得F′(x)<0,即F(x)在(-∞,0)上是减函数,
∴F(x+2017)=(x+2017)2f(x+2017),F(-2)=f(-2),
即不等式等价为F(x+2017)-F(-2)>0,
∵F(x)在(-∞,0)是减函数,
∴由F(x+2017)>F(-2)得,x+2017<-2,
即x<-2019,
故选:B.
点评 本题主要考查不等式的解法,利用条件构造函数,利用函数单调性和导数之间的关系是解决本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
5.在(2x+a)5的展开式中,含x4项的系数等于160,则${∫}_{0}^{a}$(ex+2x)dx等于( )
| A. | e2+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
13.已知函数f(x)=sin(2x+φ),其中|φ|<π,若f(x)≤|f($\frac{π}{6}$)|对x∈R恒成立,且f($\frac{π}{2}$)>f(π),则f(x)的递增区间是( )
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{2}$](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$]((k∈Z) | D. | [kπ-$\frac{π}{2}$,kπ]((k∈Z) |
17.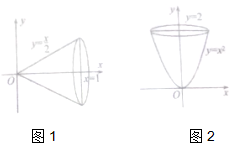 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
 如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )
如图,在平面直角坐标系xOy中,将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥,圆锥的体积V=${∫}_{0}^{1}$π($\frac{x}{2}$)2dx=$\frac{π}{12}$;据此类比,将曲线y=x2(x≥0)与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体,此旋转体的体积是( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
15.若?x>0,4a>x2-x3恒成立,则a的取值范围为( )
| A. | $({\frac{1}{27},+∞})$ | B. | $({\frac{4}{27},+∞})$ | C. | $[{\frac{1}{27},+∞})$ | D. | $[{\frac{4}{27},+∞})$ |
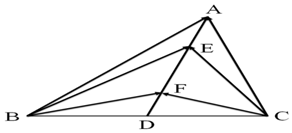 (2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,
(2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,