题目内容

9．若函数y=-x3+6x2-m的极大值为12，则实数m等于20．

分析 根据函数的极值是12，对函数求导使得导函数等于0，验证函数在这两个数字左右两边的导函数值，看出在x=4处取得极值，代入得到结果．

解答 解：∵函数y=-x3+6x2-m的极大值为12，
∴y′=-3x2+12x=0，
∴x=0，x=4，
∴函数在（0，4）上单调递增，在（4，+∞）上单调递减，
∴-64+96-m=12，
∴m=20
故答案为：20．

点评 本题考查函数的极值的应用，解题的关键是看出函数在哪一个点取得极值，代入求出结果，本题是一个基础题．

练习册系列答案
相关题目
19．已知集合{φ|f（x）=sin[（x-2φ）π]+cos[（x-2φ）π]为奇函数，且|logaφ|＜1}的子集个数为4，则a的取值范围为（$\frac{8}{13}，\frac{5}{8}$）∪（$\frac{8}{5}，\frac{13}{8}$）．
20．已知二次函数f（x）=ax2+bx+c（a，b，c∈R，a≠0），f（-2）=f（0）=0，f（x）的最小值为-1．
（1）求函数f（x）的解析式；
（2）设函数h（x）=log2[n-f（x）]，若此函数在定义域范围内不存在零点，求实数n的取值范围．
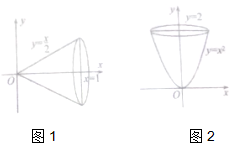17．如图，在平面直角坐标系xOy中，将直线y=$\frac{x}{2}$与直线x=1及x轴围成的封闭图形绕x轴旋转一周得到一个圆锥，圆锥的体积V=${∫}_{0}^{1}$π（$\frac{x}{2}$）2dx=$\frac{π}{12}$；据此类比，将曲线y=x2（x≥0）与直线y=2及y轴围成的封闭图形绕y旋转一周得到一个旋转体，此旋转体的体积是（　　）
A．$\frac{π}{2}$B．πC．$\frac{3π}{2}$D．2π
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率e=$\frac{1}{2}$，椭圆上的点到焦点的最小距离为1．
（1）求椭圆C的标准方程；
（2）是否存在直线l：y=kx+m（k∈R），使其与椭圆C交于A，B两点，且OA⊥OB？若存在，求出实数m的取值范围；若不存在，请说明理由．
14．（1）已知角α终边经过点P（-3，-4），求sinα，cosα，tanα的值？
（2）已知角α是第二象限角，且$sinα=\frac{3}{5}$，求cosα，tanα的值？
1．已知$f（α）=\frac{{sin（α-\frac{π}{2}）cos（\frac{3π}{2}+α）tan（π-α）}}{tan（-α-π）sin（-α-π）}，（-\frac{π}{2}＜α＜\frac{π}{2}）$
（Ⅰ）化简f（α）．
（Ⅱ）若$sin（α-\frac{π}{6}）=-\frac{1}{5}$，求$f（α+\frac{π}{3}）$的值．
18．设不等式|2x-1|＜1的解集为M，且a∈M，b∈M．
（1）试比较ab+1与a+b的大小．
（2）设max{A}表示数集A中的最大数，且$h=max\{\frac{2}{{\sqrt{a}}}，\frac{a+b}{{\sqrt{ab}}}，\frac{ab+1}{{\sqrt{b}}}\}$，求证：h＞2．
19．设函数f（x）=ln（1+x）-$\frac{2x}{x+2}$，证明：当x＞0时，f（x）＞0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网