题目内容
设函数f(x)=
+2,已知f(x)的图象与y=g(x)的图象关于直线y=x+1对称.
(1)求g(x)的解析式;
(2)解关于x的不等式:f(x)-2a≥0(其中a是常数).
| 1 |
| x |
(1)求g(x)的解析式;
(2)解关于x的不等式:f(x)-2a≥0(其中a是常数).
考点:其他不等式的解法,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)首先,设P(x,y)为y=g(x)图象上任意一点,然后,求解点P关于直线y=x+1的对称点p',最后借助于函数f(x)的解析式,确定函数g(x)的解析式;
(2)先化简给定的解析式,然后,针对a的取值情况进行讨论,注意讨论时,“不重不漏”.
(2)先化简给定的解析式,然后,针对a的取值情况进行讨论,注意讨论时,“不重不漏”.
解答:
解.(1)设(x,y)为y=g(x)图象上任意一点,
∵f(x)的图象与y=g(x)的图象关于直线y=x+1对称,
∴x+1=
+2,整理得y=
,即g(x)=
(x≠1)
(2)不等式f(x)-2a≥0?
≤0,
①当a>
时,不等式的解集为(1,
],
②当a=
时,不等式的解集为(1,+∞),
③当a<
时,不等式的解集为(-∞,
]∪(1,+∞),
综上所述,①当a>
时,不等式的解集为(1,
],
②当a=
时,不等式的解集为(1,+∞),
③当a<
时,不等式的解集为(-∞,
]∪(1,+∞).
∵f(x)的图象与y=g(x)的图象关于直线y=x+1对称,
∴x+1=
| 1 |
| y-1 |
| x |
| x-1 |
| x |
| x-1 |
(2)不等式f(x)-2a≥0?
| (2a-1)x-2a |
| x-1 |
①当a>
| 1 |
| 2 |
| 2a |
| 2a-1 |
②当a=
| 1 |
| 2 |
③当a<
| 1 |
| 2 |
| 2a |
| 2a-1 |
综上所述,①当a>
| 1 |
| 2 |
| 2a |
| 2a-1 |
②当a=
| 1 |
| 2 |
③当a<
| 1 |
| 2 |
| 2a |
| 2a-1 |
点评:本题重点考查了函数的解析式的求解方法,函数的性质及其灵活应用,注意分类讨论思想的灵活运用,属于中档题.

练习册系列答案
相关题目
方程log3x=x-3的根的情况是( )
| A、仅有一个正实数根 |
| B、有两个负根 |
| C、有一个正根和一个负根 |
| D、有两个正根 |
i为虚数,则复数(-1+i)(1+i)=( )
| A、-2+i | B、-2 |
| C、-1+i | D、-1 |
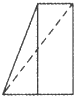
 如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正视图(或称主视图)是( )
如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正视图(或称主视图)是( )


 如图,点P(0,
如图,点P(0,