题目内容
7．集合M={x|0＜x≤3}，N={x|0＜x≤2}，则a∈M是a∈N的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 利用集合的包含关系，判断出集合M与N的关系，利用N是M的真子集，判断两者的关系．
解答 解：∵M={x|0＜x≤3}，N={x|0＜x≤2}，
∴N?M
∴“a∈M”是“a∈N”必要不充分条件．
故选B
点评 本题考查利用集合的包含关系判断一个命题是另一个命题的什么条件．当A?B时，A是B的充分不必要条件．
练习册系列答案
相关题目
15．已知函数f（x）是定义在R上的偶函数，在（-∞，0]上有单调性，且f（-2）＜f（1），则下列不等式成立的是（ ）
| A． | f（-1）＜f（2）＜f（3） | B． | f（2）＜f（3）＜f（-4） | C． | f（-2）＜f（0）＜f（$\frac{1}{2}$） | D． | f（5）＜f（-3）＜f（-1） |
2．
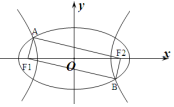如图F1、F2是椭圆C1：$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）
如图F1、F2是椭圆C1：$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{6}}{2}$ |
12．扇形的半径为1，周长为4，则扇形的圆心角弧度数的绝对值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |