题目内容
17.已知函数f(x)=sin2x+sin(2x-$\frac{π}{3}$).(1)求f(x)的最小正周期;
(2)将f(x)的图象沿x轴向左平移m(m>0)个单位,所得函数g(x)的图象关于直线x=$\frac{π}{8}$对称,求m的最小值及m最小时g(x)在$[0,\frac{π}{4}]$上的值域.
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,得出结论.
(2)利用y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用余弦函数的定义域和值域,求得g(x)在$[0,\frac{π}{4}]$上的值域.
解答 解:(1)函数$f(x)=sin2x+sin(2x-\frac{π}{3})$=sin2x+sin2xcos$\frac{π}{3}$-cos2xsin$\frac{π}{3}$
=$\frac{3}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=$\sqrt{3}$sin(2x-$\frac{π}{6}$),
∴f(x)的最小正周期为$\frac{2π}{2}$=π.
(2)将f(x)的图象沿x轴向左平移m(m>0)个单位,所得函数g(x)=$\sqrt{3}$sin(2x+2m-$\frac{π}{6}$)的图象,
根据所得图象关于直线x=$\frac{π}{8}$对称,可得$\frac{π}{4}$+2m-$\frac{π}{6}$=kπ+$\frac{π}{2}$,即m=$\frac{kπ}{2}$+$\frac{5π}{12}$,k∈Z,故m的最小值为$\frac{5π}{12}$.
此时,g(x)=$\sqrt{3}$sin(2x+$\frac{5π}{6}$-$\frac{π}{6}$)=$\sqrt{3}$sin(2x+$\frac{2π}{3}$)=$\sqrt{3}$cos(2x+$\frac{π}{6}$),
在$[0,\frac{π}{4}]$上,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],cos(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$],
∴$\sqrt{3}$cos(2x+$\frac{π}{6}$)∈[-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$],即g(x)在$[0,\frac{π}{4}]$上的值域为[-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$].
点评 本题主要考查三角恒等变换,正弦函数的周期性和图象的对称性,y=Asin(ωx+φ)的图象变换规律,余弦函数的定义域和值域,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | {5} | B. | {2,4} | C. | {2,5} | D. | {2,4,5,6} |
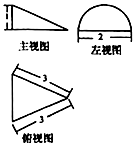
| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
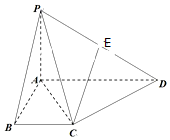 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E为PD的中点.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E为PD的中点.