题目内容
1. 如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.(1)求证:BE∥平面PAD;
(2)求证:平面PBC⊥平面PBD;
(3)设Q为棱PC上一点,$\overrightarrow{CQ}$=λ$\overrightarrow{CP}$,试确定λ的值使得二面角Q-BD-P为60°.
分析 (1)令PD中点为F,连接EF,AF,推导出四边形FABE为平行四边形,从而BE∥AF,由此能证明BE∥面PAD.
(2)过点B作BH⊥CD于H,推导出BC⊥BD.PD⊥BC,从而BC⊥平面PBD,由此能证明平面PBC⊥平面PBD.
(3)作QR⊥CD于R,作RS⊥BD于S,连结QS,则∠QSR就是二面角Q-BD-C的平面角,且∠QSR=60°,由此能求出λ的值使得二面角Q-BD-P为60°.
解答 证明:(1)令PD中点为F,连接EF,AF,
∵点E,F分别是PC、PD的中点,∴EF$\underline{\underline{∥}}$$\frac{1}{2}CD$,∴EF$\underline{\underline{∥}}$AB.
∴四边形FABE为平行四边形.∴BE∥AF,
∵AF?平面PAD,BE?平面PAD,
∴BE∥面PAD.
(2)在梯形ABCD中,过点B作BH⊥CD于H,
在△BCH中,BH=CH=1,∴∠BCH=45°.
又在△DAB中,AD=AB=1,∴∠ADB=45°,∴∠BDC=45°,
∴∠DBC=90°,∴BC⊥BD.
∵面PCD⊥面ABCD,面PCD∩面ABCD=CD,PD⊥CD,PD?面PCD,
∴PD⊥面ABCD,∴PD⊥BC,
∵BD∩PD=D,BD?平面PBD,PD?平面PBD,
∴BC⊥平面PBD,BC?平面PBC,∴平面PBC⊥平面PBD.
解:(3)作QR⊥CD于R,作RS⊥BD于S,连结QS
由于QR∥PD,∴QR⊥平面ABCD
∴∠QSR就是二面角Q-BD-C的平面角,
∵面PBD⊥面ABCD,且二面角Q-BD-P为60°
∴∠QSR=60°∴$SR=\frac{{\sqrt{3}}}{3}QR$
∵QR∥PD∴$\frac{CQ}{CP}=\frac{CR}{CD}=\sqrt{6}-2$
∴$λ=\sqrt{6}-2$.
点评 本题考查线面平行的证明,考查面面垂直的证明,考查满足条件的实数值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
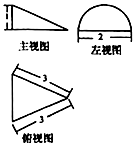
| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
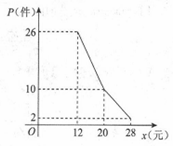 某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.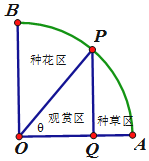 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP