题目内容

已知集合M={x|
x
x+1
＜0}，N={x|y=1gx}，则（　　）
A、N⊆MB、M⊆N
C、N∩M=∅D、N∪M=R
考点：交集及其运算
专题：集合
分析：求出M中不等式的解集确定出M，求出N中x的范围确定出N，即可做出判断．
解答： 解：由M中不等式变形得：x（x+1）＜0，
解得：-1＜x＜0，即M={x|-1＜x＜0}，
由N中y=lgx，得到x＞0，即N={x|x＞0}，
则M∩N=∅．
故选：C．
点评：此题考查了交集及其运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
若对任意x＞0，a≥
3
x
x2-3x+3
恒成立，则a的取值范围是
 
．
比较大小 log20.5
 
log0.20.1．
在长方体ABCD-A1B1C1D1中，AB=2，AD=2，CC1=，则二面角C1-BD-C的大小为
 
．
已知集合M={-1，1}，N={-1，0，2}，则M∩N为（　　）
A、{-1，1}B、{-1}
C、{0}D、{-1，0}
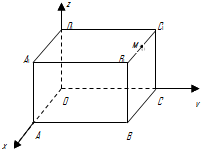如图所示的空间直角坐标系O-xyz下，长方体OABC-D1A1B1C1中，|OA|=3，|OC|=4，|OD1|=2，则B1C1的中点M的坐标是（　　）
A、（
3
2
，4，2）
B、（3，2，2）
C、（3，4，1）
D、（
3
2
，2，1）
直线2x+3y+1=0与直线4x+my+7=0平行，则它们之间的距离为（　　）
A、4
B、
2
13
13
C、
5
26
13
D、
7
20
10
若函数f（x）=a|x-b|+2在[0，+∞）上为增函数，则实数a，b的取值范围是（　　）
A、a＞0，b＜0
B、a＞0，b≤0
C、a＜0，b≤0
D、a=1，b≥0
已知向量
a
=（1，1），
b
=（2，x），若
a
+
b
∥4
b
-2
a
，则实数x的值是（　　）
A、-2B、0C、1D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网