题目内容
7.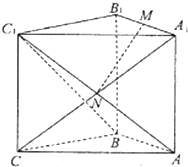 直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.
直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,M为A1B1的中点,N是AC1与A1C的交点.(Ⅰ)求证:MN∥平面BCC1B1;
(Ⅱ)求证:MN⊥平面ABC1.
分析 (Ⅰ)证明线面平行,只需证明MN平行于平面BCC1B1内的一条直线,利用三角形的中位线可证;
(Ⅱ)由B1C⊥BC1.则AB⊥平面BCC1B1,B1C⊥AB,则B1C⊥平面ABC1,则MN∥B1C,即可证明MN⊥平面ABC1.
解答 解:(Ⅰ)证明:连结B1C,由M,N分别为A1B1,A1C的中点,
∴MN∥B1C,
由MN?平面BCC1B1,B1C?平面BCC1B1,
∴MN∥平面BCC1B1,
(Ⅱ)证明:∵在直三棱柱中BC=BB1,
∴侧面BCC1B1为正方形,则B1C⊥BC1.
∵AB⊥BC,AB⊥BB1,BC∩BB1=B,
BC?平面BCC1B1,BB1?平面BCC1B1,
∴AB⊥平面BCC1B1.
∵B1C?平面BCC1B1,
∴B1C⊥AB,
∵AB∩BC1=B,
∴B1C⊥平面ABC1,
∵MN∥B1C,
∴MN⊥平面ABC1.
点评 本题主要考查了直线与平面垂直的判定,空间中直线与直线之间的位置关系,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知函数f(x)=$\frac{lnx}{x}$,若方程f(x)=m存在两个不同的实数解,则实数m的取值范围为( )
| A. | (0,$\frac{1}{e}$) | B. | (0,e) | C. | (-∞,$\frac{1}{e}$) | D. | (0,$\frac{1}{e}$] |
2.同时抛掷三枚均匀的硬币,则基本事件的总个数和恰有2个正面朝上的基本事件的个数分别为( )
| A. | 3,3 | B. | 4,3 | C. | 6,3 | D. | 8,3 |
19.把长为80cm的铁丝随机截成三段,则每段铁丝长度都不小于20cm的概率是( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{16}$ |
17.某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
附:b=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,a=$\overline y$-b$\overline x$.
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 56 | 50 | 48 | 45 |
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
附:b=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,a=$\overline y$-b$\overline x$.
 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,E,F分别为AD,PC的中点.