题目内容
19．把长为80cm的铁丝随机截成三段，则每段铁丝长度都不小于20cm的概率是（ ）| A． | $\frac{1}{16}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{16}$ |
分析 设把长为80cm的铁丝随机截成三段的长度分别为x，y，80-x-y，则由题意知$\left\{\begin{array}{l}{80≥x≥20}\\{80≥y≥20}\\{80≥80-x-y≥20}\end{array}\right.$，以面积为测度，即可求出概率．
解答 解：设把长为80cm的铁丝随机截成三段的长度分别为x，y，80-x-y，
则由题意知$\left\{\begin{array}{l}{80≥x≥20}\\{80≥y≥20}\\{80≥80-x-y≥20}\end{array}\right.$，
所以包含事件每段铁丝长度都不小于20cm所表示的面积为区域的面积为$\frac{1}{2}×20×20$=200，
而基本事件所表示的平面$\frac{1}{2}×$80×80=3200，
所以由几何概型的计算公式即可得出每段铁丝长度都不小于20cm的概率为$\frac{1}{16}$．
故选A．
点评 本题考查几何概型，考查面积的计算，属于中档题．
练习册系列答案
相关题目
10．设A，B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴两端点，Q为椭圆上一点，使∠AQB=120°，则椭圆离心率e的取值范围为（ ）
| A． | [$\frac{\sqrt{3}}{2}$，1） | B． | [$\frac{\sqrt{6}}{3}$，1） | C． | （0，$\frac{\sqrt{3}}{2}$] | D． | （0，$\frac{\sqrt{6}}{3}$] |
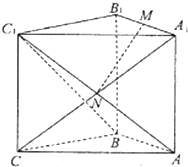直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=BB1，M为A1B1的中点，N是AC1与A1C的交点．
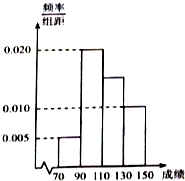某班一次数学考试成绩频率分布直方图如图所示，数据分组依次为[70，90），[90，110），[110，130），[130，150]，已知成绩大于等于90分的人数为36人，现采用分层抽样的方式抽取一个容量为10的样本．